Overview of Available Algorithms.

In many cases we can transform the pencil (5.1) into a standard HEP discussed in Chapter 4, or in some cases into a standard NHEP discussed in Chapter 7, and use any of the algorithms described in these two chapters. We give a short review of such transformations in §5.2.

The main body of this chapter is devoted to algorithms that take a special form for generalized Hermitian pencils (5.1):

Power method and inverse iteration,

§5.4, is the basic iterative method. It starts with an appropriate starting vector and makes one matrix-vector multiplication and one linear system solve in each iteration. Needing both these operations, it is less appealing than in the standard case, but it is included here because of its simplicity and to clarify its relations to more sophisticated schemes described later.

Lanczos method,

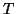§5.5, builds up a $B$ orthogonal basis of a Krylov sequence of vectors in which the matrix operator is represented by a tridiagonal matrix $T$, whose eigenvalues yield Ritz approximations to several of the eigenvalues of the original matrix pencil (5.1). 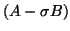We will describe two variants in §5.5, one direct iteration that needs multiplications with $A$ and the solution of systems with $B$, and one shift-and-invert iteration that needs solution of systems with $(A-\sigma B)$ and multiplication with $B$.

Jacobi-Davidson method,

§5.6, updates a sequence of subspaces, operating with a preconditioned shifted matrix. It uses $B$ orthogonality and does not need the solution of linear systems. This makes it applicable in several cases when the matrices are too large to allow for solving linear systems, as needed in the other algorithms described in this chapter.