




Next: Computing Interior Eigenvalues
Up: Restart and Deflation
Previous: Preconditioning.
Contents
Index
The complete algorithm for the Jacobi-Davidson method that includes
restart with a number of Ritz vectors and deflation for the computation
of a number of eigenpairs is called JDQR [172], since it can be
interpreted as an iterative approach for the QR algorithm. The template
for this algorithm is given in Algorithm 4.17.

To apply this algorithm we need to specify a starting vector 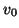 , a
tolerance
, a
tolerance 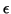 , a target value
, a target value 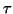 , and a number
, and a number 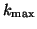 that specifies how many eigenpairs near
that specifies how many eigenpairs near 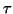 should be computed. The
value of
should be computed. The
value of 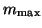 denotes the maximum dimension of the search
subspace. If it is exceeded, a restart takes place with a subspace
of specified dimension
denotes the maximum dimension of the search
subspace. If it is exceeded, a restart takes place with a subspace
of specified dimension 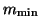 .
.
On completion typically the 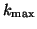 largest eigenvalues are delivered when
largest eigenvalues are delivered when
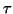 is chosen larger than
is chosen larger than
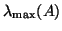 ;
the
;
the 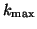 smallest
eigenvalues are delivered if
smallest
eigenvalues are delivered if 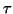 is chosen smaller than
is chosen smaller than
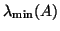 . The computed eigenpairs
. The computed eigenpairs
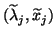 ,
,
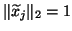 ,
satisfy
,
satisfy
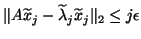 , where
, where
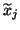 denotes the
denotes the  th column of
th column of 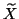 .
.
In principle, this algorithm computes the 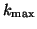 eigenvalues
closest to a specified target value
eigenvalues
closest to a specified target value 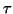 . This is only reliable if the
. This is only reliable if the
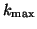 largest or
largest or 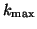 smallest eigenvalues are wanted. For
interior sets of eigenvalues we will describe safer techniques in
§4.7.4. We will now comment on some parts of the
algorithm in view of our discussions in previous subsections.
smallest eigenvalues are wanted. For
interior sets of eigenvalues we will describe safer techniques in
§4.7.4. We will now comment on some parts of the
algorithm in view of our discussions in previous subsections.
- (2)
- Initialization phase. The search subspace is initialized with
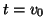 .
.
- (4)-(6)
- The new expansion vector for the search subspace is made orthogonal with
respect to the current search subspace by means of modified
Gram-Schmidt. This can be replaced, for improved numerical stability, by
the template given in Algorithm 4.14.
If 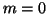 , this is an empty loop.
, this is an empty loop.
- (8)-(10)
- We compute only the upper triangular part of the
Hermitian matrix
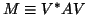 (of order
(of order 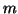 ).
).
- (11)
- The eigenproblem for the
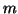 by
by 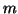 matrix
matrix 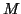 can be solved by a
standard eigensolver for dense Hermitian eigenproblems from LAPACK. We
have chosen to compute the standard Ritz values, which makes the
algorithm suitable for computing the largest or smallest
can be solved by a
standard eigensolver for dense Hermitian eigenproblems from LAPACK. We
have chosen to compute the standard Ritz values, which makes the
algorithm suitable for computing the largest or smallest 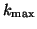 eigenvalues of
eigenvalues of  . If one wishes to compute
. If one wishes to compute 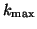 eigenvalues
somewhere in the interior of the spectrum, the usage of harmonic
Ritz values is advocated; see §4.7.4.
eigenvalues
somewhere in the interior of the spectrum, the usage of harmonic
Ritz values is advocated; see §4.7.4.
The matrix 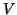 denotes the
denotes the  by
by 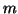 matrix with columns
matrix with columns 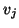 ,
,
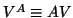 likewise;
likewise; 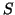 is the
is the  by
by  matrix
with columns
matrix
with columns 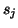 ,
and
,
and
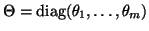 .
.
- (13)
- The stopping criterion is to accept an eigenvector approximation as soon
as the norm of the residual (for the normalized eigenvector
approximation) is below
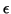 . This means that we accept
inaccuracies the order of
. This means that we accept
inaccuracies the order of 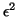 in the computed eigenvalues
and inaccuracies (in angle) in the eigenvectors in the order of
in the computed eigenvalues
and inaccuracies (in angle) in the eigenvectors in the order of
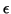 , provided that the associated eigenvalue is simple and well
separated from the other eigenvalues; see (4.4).
, provided that the associated eigenvalue is simple and well
separated from the other eigenvalues; see (4.4).
Occasionally one of the wanted eigenvectors of  may be undetected,
for instance, if
may be undetected,
for instance, if 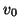 has no component in the corresponding eigenvector
direction. For a random start vector this is rather unlikely.
(See also note (14) for Algorithm 4.13.)
has no component in the corresponding eigenvector
direction. For a random start vector this is rather unlikely.
(See also note (14) for Algorithm 4.13.)
- (16)
- After acceptance of a Ritz pair, we continue the search for a next
eigenpair, with the remaining Ritz vectors as a basis for the initial
search space. These vectors are computed in (17)-(20).
- (23)
- We restart as soon as the dimension of the search space for the current
eigenvector exceeds
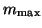 . The process is restarted with the
subspace spanned by the
. The process is restarted with the
subspace spanned by the 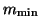 Ritz vectors corresponding to the Ritz
values closest to the target value
Ritz vectors corresponding to the Ritz
values closest to the target value 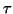 (and
they are computed lines (25)-(27)).
(and
they are computed lines (25)-(27)).
- (30)-(31)
- We have collected the locked (computed)
eigenvectors in
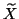 , and the
matrix
, and the
matrix 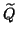 is
is 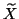 expanded with the current eigenvector
approximation
expanded with the current eigenvector
approximation 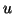 . This is done in order to obtain a more compact
formulation; the correction equation is equivalent to the one
in (4.50). The new correction
. This is done in order to obtain a more compact
formulation; the correction equation is equivalent to the one
in (4.50). The new correction 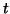 has to be orthogonal to
the columns of
has to be orthogonal to
the columns of 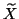 as well as to
as well as to 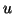 .
.
Of course, the correction
equation can be approximately solved by any suitable process, for instance,
by a preconditioned Krylov subspace method. Because of the occurrence of
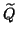 one has to be careful with the use of preconditioners
for the matrix
one has to be careful with the use of preconditioners
for the matrix 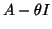 . The inclusion of preconditioners can be
done following the same principles as for the single-vector
Jacobi-Davidson algorithm; see Algorithm 4.18 for a template.
Make sure that the starting vector
. The inclusion of preconditioners can be
done following the same principles as for the single-vector
Jacobi-Davidson algorithm; see Algorithm 4.18 for a template.
Make sure that the starting vector 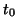 for an iterative solver
satisfies the orthogonality constraints
for an iterative solver
satisfies the orthogonality constraints
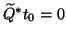 .
Note that significant savings per step can be made in
Algorithm 4.18 if
.
Note that significant savings per step can be made in
Algorithm 4.18 if 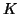 is kept the same for a (few)
Jacobi-Davidson iterations. In that case columns of
is kept the same for a (few)
Jacobi-Davidson iterations. In that case columns of 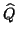 can
be saved from previous steps. Also the matrix
can
be saved from previous steps. Also the matrix 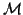 in
Algorithm 4.18 can be updated from previous steps, as well as
its
in
Algorithm 4.18 can be updated from previous steps, as well as
its
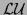 decomposition.
decomposition.






Next: Computing Interior Eigenvalues
Up: Restart and Deflation
Previous: Preconditioning.
Contents
Index
Susan Blackford
2000-11-20

![]() , a
tolerance
, a
tolerance ![]() , a target value
, a target value ![]() , and a number
, and a number ![]() that specifies how many eigenpairs near
that specifies how many eigenpairs near ![]() should be computed. The
value of
should be computed. The
value of ![]() denotes the maximum dimension of the search
subspace. If it is exceeded, a restart takes place with a subspace
of specified dimension
denotes the maximum dimension of the search
subspace. If it is exceeded, a restart takes place with a subspace
of specified dimension ![]() .
.
![]() largest eigenvalues are delivered when
largest eigenvalues are delivered when
![]() is chosen larger than
is chosen larger than
![]() ;
the
;
the ![]() smallest
eigenvalues are delivered if
smallest
eigenvalues are delivered if ![]() is chosen smaller than
is chosen smaller than
![]() . The computed eigenpairs
. The computed eigenpairs
![]() ,
,
![]() ,
satisfy
,
satisfy
![]() , where
, where
![]() denotes the
denotes the ![]() th column of
th column of ![]() .
.
![]() eigenvalues
closest to a specified target value
eigenvalues
closest to a specified target value ![]() . This is only reliable if the
. This is only reliable if the
![]() largest or
largest or ![]() smallest eigenvalues are wanted. For
interior sets of eigenvalues we will describe safer techniques in
§4.7.4. We will now comment on some parts of the
algorithm in view of our discussions in previous subsections.
smallest eigenvalues are wanted. For
interior sets of eigenvalues we will describe safer techniques in
§4.7.4. We will now comment on some parts of the
algorithm in view of our discussions in previous subsections.
![]() , this is an empty loop.
, this is an empty loop.
![]() denotes the
denotes the ![]() by
by ![]() matrix with columns
matrix with columns ![]() ,
,
![]() likewise;
likewise; ![]() is the
is the ![]() by
by ![]() matrix
with columns
matrix
with columns ![]() ,
and
,
and
![]() .
.
![]() may be undetected,
for instance, if
may be undetected,
for instance, if ![]() has no component in the corresponding eigenvector
direction. For a random start vector this is rather unlikely.
(See also note (14) for Algorithm 4.13.)
has no component in the corresponding eigenvector
direction. For a random start vector this is rather unlikely.
(See also note (14) for Algorithm 4.13.)
![]() one has to be careful with the use of preconditioners
for the matrix
one has to be careful with the use of preconditioners
for the matrix ![]() . The inclusion of preconditioners can be
done following the same principles as for the single-vector
Jacobi-Davidson algorithm; see Algorithm 4.18 for a template.
Make sure that the starting vector
. The inclusion of preconditioners can be
done following the same principles as for the single-vector
Jacobi-Davidson algorithm; see Algorithm 4.18 for a template.
Make sure that the starting vector ![]() for an iterative solver
satisfies the orthogonality constraints
for an iterative solver
satisfies the orthogonality constraints
![]() .
Note that significant savings per step can be made in
Algorithm 4.18 if
.
Note that significant savings per step can be made in
Algorithm 4.18 if ![]() is kept the same for a (few)
Jacobi-Davidson iterations. In that case columns of
is kept the same for a (few)
Jacobi-Davidson iterations. In that case columns of ![]() can
be saved from previous steps. Also the matrix
can
be saved from previous steps. Also the matrix ![]() in
Algorithm 4.18 can be updated from previous steps, as well as
its
in
Algorithm 4.18 can be updated from previous steps, as well as
its
![]() decomposition.
decomposition.