
Figure 5: The X11 Interface (XI) and SDC
To take advantage of the graphical nature of the spectral decomposition process, a graphical user interface (GUI) has been implemented for SDC. Written in C and based on X11R5's standard Xlib library, the Xt toolkit and MIT's Athena widget set, it has been nicknamed XI for ``X11 Interface''. When XI is paired with code implementing SDC we call the union XSDC.
The programmer's interface to XI consists of seven subroutines designed independently of any specific SDC implementation. Thus XI can be attached to any SDC code. At present, it is in use with the CM-5 CMF/CMSSL implementation and the Fortran 77 version of our algorithm (both of which use real arithmetic only). Figure 1 shows the coupling of the SDC code and the XI library of subroutines.

Figure 5: The X11 Interface (XI) and SDC
Basically, the SDC code calls an XI routine which handles all interaction with the user and returns only when it has the next request for a parallel computation. The SDC code processes this request on the parallel engine, and if necessary calls another XI routine to inform the user of the computational results. If the user had selected to split the spectrum, then at this point the size of the highlighted region, and the error bound on the computation (along with some performance information) is reported, and the user is given the choice of confirming or refusing the split. Appropriate action is taken depending on the choice. This process is repeated until the user decides to terminate the program.
All data structures pertaining to the matrix decomposition process are managed by XI. A binary tree records the size and status (solved/not solved) of each diagonal block corresponding to a spectral region, the error bounds of each split, and other information. Having the X11 interface manage the decomposition data frees the SDC programmer of these responsibilities and encapsulates the decomposition process. The SDC programmer obtains any useful information via the interface subroutines.

Figure 6: A sample xsdc session
Figure 6 pictures a sample session of xsdc
on the CM-5 with a 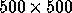 matrix.
The large, central window (called the ``spectrum window'')
represents the region of the complex plane indicated by the axes.
Its title - ``xsdc :: Eigenvalues and Schur Vectors" -
indicates that the task is to compute eigenvalues and
Schur vectors for the matrix under analysis.
The lines on the spectrum window (other than the axes) are the result
of spectral divide and conquer, while the shading indicates that the ``bowtie''
region of the complex plane is currently selected for further analysis.
The other windows (which can be raised/lowered at the user's
request) show the details
of the process and will be described later.
matrix.
The large, central window (called the ``spectrum window'')
represents the region of the complex plane indicated by the axes.
Its title - ``xsdc :: Eigenvalues and Schur Vectors" -
indicates that the task is to compute eigenvalues and
Schur vectors for the matrix under analysis.
The lines on the spectrum window (other than the axes) are the result
of spectral divide and conquer, while the shading indicates that the ``bowtie''
region of the complex plane is currently selected for further analysis.
The other windows (which can be raised/lowered at the user's
request) show the details
of the process and will be described later.
The buttons at the top control I/O, the appearance of the spectrum window, and algorithmic choices:
The buttons at the bottom are used in splitting the spectrum. For example
clicking on Right halfplane and then clicking at any point on the
spectrum window
will split the spectrum into two halfplanes at that point, with the
right halfplane selected for further division.
This would signal the SDC code to decompose the matrix  to
to
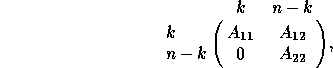
where the  eigenvalues of
eigenvalues of 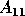 are the eigenvalues of
are the eigenvalues of 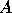 in the
right halfplane, and the eigenvalues of
in the
right halfplane, and the eigenvalues of 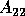 are
the eigenvalues of
are
the eigenvalues of 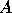 in the left halfplane.
The button Left Halfplane
works similarly, except that the left halfplane would
then be selected for further processing and the roles of
in the left halfplane.
The button Left Halfplane
works similarly, except that the left halfplane would
then be selected for further processing and the roles of 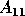 and
and 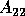 would be reversed.
In the same manner, Inside Circle and Outside Circle
divide the complex plane at the boundary of a circle,
while East-West Crosslines and North-South Crosslines
split the spectrum with lines at 45 degrees to the real axis (described below).
would be reversed.
In the same manner, Inside Circle and Outside Circle
divide the complex plane at the boundary of a circle,
while East-West Crosslines and North-South Crosslines
split the spectrum with lines at 45 degrees to the real axis (described below).
The Split Information window in the lower right
corner of Figure 2 keeps track of the matrix splitting process.
It reports the two splits performed to arrive at this current
(shaded) spectral region.
The first, an East-West Crossline split at the point 1.5
on the real axis, divided the entire complex plane into four sectors by
drawing two lines at  45 degrees through the point 1.5 on the
real axis. SDC decomposed the starting matrix into:
45 degrees through the point 1.5 on the
real axis. SDC decomposed the starting matrix into:
where the East and West sectors correspond to
the 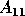 block
while the North and South sectors correspond to the
block
while the North and South sectors correspond to the
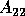 block.
block.
Continuing in the East-West sectors as indicated by the previous split, that region is divided into two sub-regions separated by the boundary of the circle of radius 4 centered at the origin. The circle is drawn, making sure that its boundary only intersects the East and West sectors, and the matrix is reduced to:
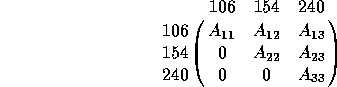
The shading indicates that the ``bowtie'' region (corresponding to
the interior of the circle, and the 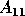 block)
is currently selected for further analysis.
block)
is currently selected for further analysis.
In the upper right corner of Figure 2 the Matrix Information window
displays the status of the matrix decomposition process.
Each of the three entries corresponds to a spectral region and a square
diagonal block of the 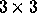 block upper triangular matrix,
and informs us of the block's size, whether
its eigenvalues (eigenvectors, Schur vectors) have been
computed or not,
and the maximum error bound encountered along
this path of the decomposition process.
The highlighted entry corresponds to the shaded region and
reports that the
block upper triangular matrix,
and informs us of the block's size, whether
its eigenvalues (eigenvectors, Schur vectors) have been
computed or not,
and the maximum error bound encountered along
this path of the decomposition process.
The highlighted entry corresponds to the shaded region and
reports that the 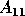 block contains 106 eigenvalues,
has been solved, and is in error
by up to
block contains 106 eigenvalues,
has been solved, and is in error
by up to 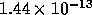 . The eigenvalues - listed in the window
overlapping the Matrix Information window -
can be plotted on the spectrum at the user's request.
. The eigenvalues - listed in the window
overlapping the Matrix Information window -
can be plotted on the spectrum at the user's request.
The user may select any region of the complex plane (and hence
any sub-matrix on the diagonal) for further decomposition by
clicking the pointer in the desired region.
A click at the point 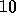 on the imaginary axis for example,
would unhighlight the current region and shade the North and South sectors.
Since this region corresponds to the
on the imaginary axis for example,
would unhighlight the current region and shade the North and South sectors.
Since this region corresponds to the 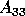 block,
the third entry in the Matrix-Information window would be highlighted.
The Split-Information window would also be updated to detail
the single split performed in arriving at this region of the spectrum.
block,
the third entry in the Matrix-Information window would be highlighted.
The Split-Information window would also be updated to detail
the single split performed in arriving at this region of the spectrum.
Once a block is small enough, the user may choose to solve it (via the Function button at the top of the spectrum window). In this case the eigenvalues, and Schur vectors for that block would be computed using QR (as per the user's request) and the eigenvalues plotted on the spectrum.
The current XI code supports real SDC only. It will be extended to handle the complex case as implementations of complex SDC become available.