Performance Model  

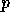
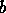
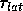
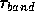
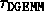
Our model is based on the actual operation counts of the ScaLAPACK implementation and the following problem parameters and (measured) machine parameters.

Matrix size


Number of processors


Block size (in the 2D block cyclic matrix data layout) [20]


Time required to send a zero length message from one processor to another.


Time required to send one double word from one processor to another.


Time required per BLAS 3 floating point operation

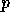
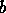
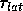
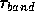
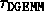
Models for each of the building blocks are given in Table 4. Each model was created by counting the actual operations in the critical path. The load imbalance cost represents the discrepancy between the amount of work which the busiest processor must perform and the amount of work which the other processors must perform. Each of the models for the building blocks were validated against the performance data shown in the appendix. The load imbalance increases as the block size increases.

 
Table 4:   Models for each of the building blocks

 
Table 5:   Model of Algorithm 1

Because it is based on operation counts, we can not only predict performance, but also estimate the importance of various suggested modifications either to the algorithm, the implementation or the hardware. In general, predicting performance is risky because there are so many factors which control actual performance, including the compiler and various library routines. However, since the majority of the time spent in Algorithm 1 is spent in either the BLACS or the level 3 PB-BLAS[15] (which are in turn implemented as calls to the BLACS[25] and the BLAS[22][23][38]), as long as the performance of the BLACS and the BLAS are well understood and the input matrix is not too small, we can predict the performance of Algorithm 1 on any distributed memory parallel computer. In Table 5, the predicted running time of each of the steps of Algorithm 1 is displayed. Summing the times in Table 5 yields:

Using the measured machine parameters given in Table 8 with equation (4.9) yields the predicted times in Table 7 and Table 3. To get Table 4 and Table 5 and hence equation (4.9), we have made a number of simplifying assumptions based on our empirical results. We assume that 20 Newton iterations are required. We assume that the time required to send a single message of 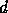double words is 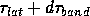, regardless of how many messages are being sent in the system. Although there are many patterns of communication in the ScaLAPACK implementation, the majority of the communication time is spent in collective communications, i.e. broadcasts and reductions over rows or columns. We therefore choose 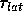and 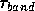based on programs that measure the performance of collective communications. We assume a perfectly square 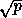-by-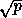 processor grid. These assumptions allow us to keep the model simple and understandable, but limit its accuracy somewhat.

As Tables 6 and 7 show, our model underestimates the actual time on the Delta by no more than 20% for the machine and problem sizes that we timed. Table 3 shows that our model matches the performance on the CM5 to within 25% for all problem sizes except the smallest, i.e. .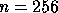

  
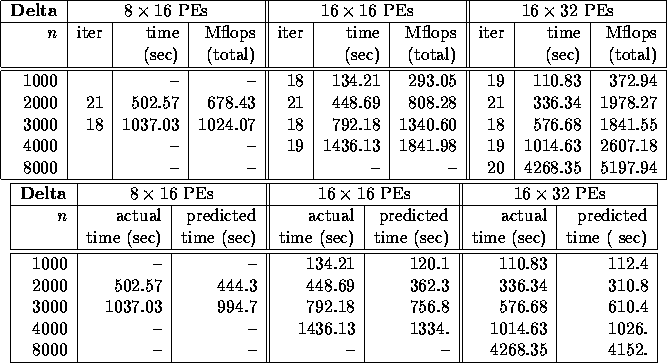
Table 7: Predicted performance of the Newton iteration based algorithm (Algorithm 1) for the spectral decomposition along the pure imaginary axis.  

Table 6: Performance of the Newton iteration based algorithm (Algorithm 1) for the spectral decomposition along the pure imaginary axis, all backward errors .  

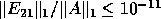The main sources of error in our model are:

1. uncounted operations, such as small BLAS 1 and BLAS 2 calls, data copying and norm computations,

2. non-square processor configurations,

3. differing numbers of Newton iterations required

4. communications costs which do not fit our linear model,

5. matrix multiply costs which do not fit our constant cost/flop model, and

6. the higher cost of QR decomposition with pivoting.

Data layout, i.e. the number of processor rows and processor columns and the block size, is critical to the performance of this algorithm. We assume an efficient data layout. Specifically that means a roughly square processor configuration and a fairly large block size (say 16 to 32). The cost of redistributing the data on input to this routine would be tiny, 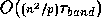, compared to the total cost of the algorithm.

The optimal data layout for LU decomposition is different from the optimal data layout for computi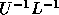ng . The former prefers slightly more processor rows than columns while the latter prefers slightly more processor columns than rows. In addition, LU decomposition works best with a small block size, 6 on the Delta for example, whereas computing 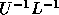is best done with a large block size, 30 on the Delta for example. The difference is significant enough that we believe a slight overall performance gain, maybe 5% to 10%, could be achieved by redistributing the data between these two phases, even though this redistribution would have to be done twice for each Newton step.

Table 3 shows that except for 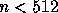our model estimates the performance Algorithm 1 based on CMSSL reasonably well. Note that this table is for a Newton-Shultz iteration scheme which is slightly more efficient on the CM5 than the Newton based iteration. This introduces another small error. The fact that our model matches the performance of the CMSSL based routine, whose internals we have not examined, indicates to us that the implementation of matrix inversion on the CM5 probably requires roughly the same operation counts as the ScaLAPACK implementation.

 
Table 8:   Machine parameters

The performance figures in Table 8 are all measured by an independent program, except for the CM5 BLAS 3 performance. The communication performance figures for the Delta in Table 8 are from a report by Littlefield[43]. The communication performance figures for the CM5 are as measured by Whaley[58]. The computation performance for the Delta is from the Linpack benchmark[21] for a 1 processor Delta. There is no entry for a 1 processor CM5 in the Linpack benchmark, so 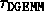in Table 8 above is chosen from our own experience.