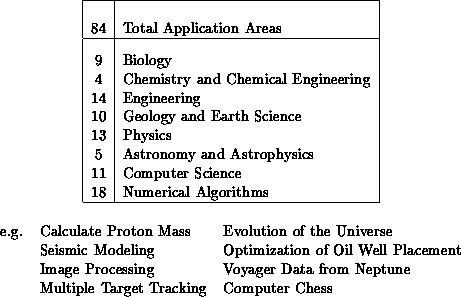
Table 14.1: 84 Application Areas Used in a Survey 1988-89 from 400 Papers






Table 14.1: 84 Application Areas Used in a Survey 1988-89 from 400 Papers
The two applications in this chapter fall into the asynchronous problem class of Section 3.4. This class is caricatured in Figure 14.1 and is the last and hardest to parallelize of the basic problem architectures introduced in Section 3.4. Thus, we will use this opportunity to summarize some issues across all problem classes. It would be more logical to do this in Chapter 18 where we discuss the compound metaproblem class, which we now realize is very important. However, the discussion here is based on a survey [Fox:88b], [Angus:90a] undertaken from 1988 to 1989, at which time we had not introduced the concept of compound or hierarchical problem architectures.
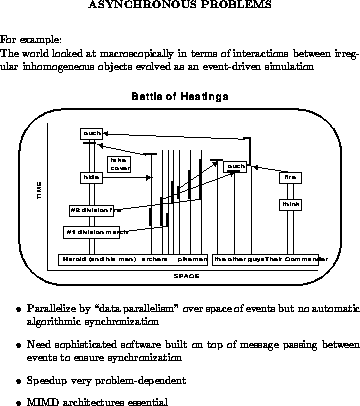
Figure 14.1: The Asynchronous Problem Class
Table 14.1 divides 84 application areas into eight (academic)
disciplines. Examples of the areas are given in the table-essentially each
application section in this book would lead to a separate area for the purposes
of this table.
These areas are listed in [Angus:90a], [Fox:88b;92b]
and came a reading in 1988 of about 400 papers which
had developed quite seriously a parallel application or core
nontrivial algorithm. In 1988, it was possible to read essentially
all such papers-the field has grown so much in the following years
that a complete survey would now be a daunting task.
Table 14.2 divides these application areas into the basic
problem architectures used in the book. There are several caveats to
be invoked for this table. As we have seen in Chapters 9 and
12, the division between synchronous and loosely
synchronous is not sharp and is still a matter of important debate. The
synchronous problems are naturally suitable for SIMD architectures,
while properly loosely synchronous and asynchronous problems require
MIMD hardware. This classification is illustrated by a few of the more
major C P applications in Table 14.3 [Fox:89t],
which also compares performance on various SIMD and MIMD machines in
use in 1989.
P applications in Table 14.3 [Fox:89t],
which also compares performance on various SIMD and MIMD machines in
use in 1989.
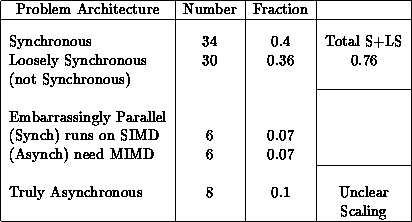
Table 14.2: Classification of 400 Applications in 84 Areas from 1989.
90% of applications scale to large SIMD/MIMD machines.
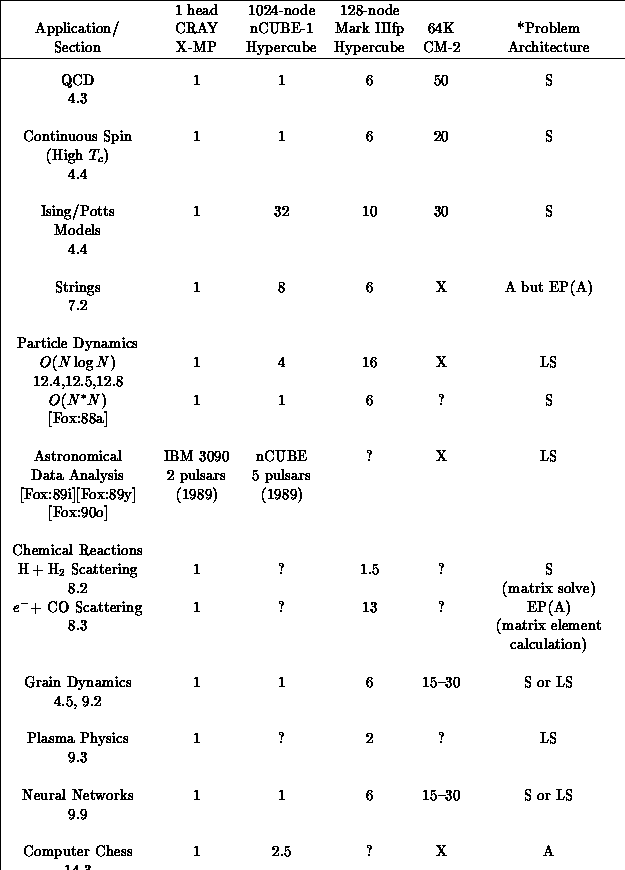
Table 14.3: Classification of some C P applications from 1989 and
their performances on machines at that time [Fox:89t]. A question mark
indicates the performance is unknown whereas an X indicates we expect or
have measured poor performance.
P applications from 1989 and
their performances on machines at that time [Fox:89t]. A question mark
indicates the performance is unknown whereas an X indicates we expect or
have measured poor performance.
Table 14.2 can be interpreted as follows: 90% of application areas (i.e., all except the asynchronous class) naturally parallelize to large numbers of processors.
Forty-seven percent of applications will run well on SIMD machines while 43% need a MIMD architecture (this is a more precise version of Equation 3.21).
These numbers are rough for many reasons. The grey line between synchronous (perhaps generalized to autonomous SIMD in Maspar language of Section 6.1) and loosely synchronous means that the division between SIMD and MIMD fractions is uncertain. Further, how should one weight each area? QCD of Section 4.3 is one of the application areas in Table 14.1, but this uses an incredible amount of computer time and is a synchronous problem. Thus, weighting by computer cycles needed or used could also change the ratios significantly.
These tables can also be used to discuss software issues as described in Sections 13.1 and 18.2. The synchronous and embarrassingly parallel problem classes (54%) are those directly supported by the initial High Performance Fortran language [Fox:91e], [Kennedy:93a]. The loosely synchronous problems (34%) need run-time and language extensions, which we are currently working on [Berryman:91a], [Saltz:91b], [Choudhary:92d], as mentioned in Section 13.1 (Table 13.4). With these extensions, we expect High Performance Fortran to be able to express nearly all synchronous, loosely synchronous, and embarrassingly parallel problems.
The fraction (10%) of asynchronous problems is in some sense pessimistic. There is one very important asynchronous area-event driven simulations-where the general scaling parallelism remains unclear. This is illustrated in Figure 14.1 and briefly discussed in Section 15.3. However, the two cases described in this chapter parallelize well-albeit with very hard work from the user! Further, some of the asynchronous areas in Tables 14.1 and 14.2 are of the compound class of Chapter 18 and these also parallelize well.
The two examples in this chapter need different algorithmic and software support. In fact, as we will note in Section 15.1, one of the hard problems in parallel software is to isolate those issues that need to be supported over and above those needed for synchronous and loosely synchronous problems. The software models needed for irregular statistical mechanics (Section 14.2), chess (Section 14.3), and event-driven simulations (Section 15.3) are quite different.
In Section 14.2, the need for a sequential ordering takes the normally loosely synchronous time-stepped particle dynamics into an asynchronous class. Time-stamping the updates provides the necessary ordering and a ``demand-driven processing queue'' provides scaling parallelism. Communication must be processed using interrupts and the loosely synchronous communication style of Section 9.1 will not work.
Another asynchronous application developed by C P was the ray-tracing
algorithm developed by Jeff Goldsmith and John Salmon
[Fox:87c],
[Goldsmith:87a;88a]. This application used
two forms of parallelism, with both the pixels (rays) and the basic
model to be rendered distributed. This allows very large models to be
simulated and the covers of our earlier books [Fox:88a],
[Angus:90a] feature pictures rendered by this program. The
distributed-model database requires software support similar to that
of the application in Section 14.2. The rays migrate from
node to node as they traverse the model and need to access data not
present in the node currently responsible for ray. This application
was a great technical success, but was not further developed as it
used software (MOOSE of Section 15.2) which was only
supported on our early machines. The model naturally forms a tree
with the scene represented with increasing spatial resolution as you
go down the different levels of the tree. Goldsmith and Salmon used a
similar strategy to the hierarchical Barnes-Hut approach to particle
dynamics described in Section 12.4. In particular, the upper
parts of the tree are replicated in all nodes and only the lower parts
distributed. This removes ``sequential bottlenecks'' near the top of the tree just as in the astrophysics case.
Originally, Salmon's thesis intended to study the computer science and
science issues associated with hierarchical data structures.
Multiscale methods are pervasive to essentially all
physical systems. However, the success of the astrophysical
applications led to this being his final thesis topic. Su, another
student of Fox, has just finished his Ph.D. on the general mathematical
properties of hierarchical systems [Su:93a].
P was the ray-tracing
algorithm developed by Jeff Goldsmith and John Salmon
[Fox:87c],
[Goldsmith:87a;88a]. This application used
two forms of parallelism, with both the pixels (rays) and the basic
model to be rendered distributed. This allows very large models to be
simulated and the covers of our earlier books [Fox:88a],
[Angus:90a] feature pictures rendered by this program. The
distributed-model database requires software support similar to that
of the application in Section 14.2. The rays migrate from
node to node as they traverse the model and need to access data not
present in the node currently responsible for ray. This application
was a great technical success, but was not further developed as it
used software (MOOSE of Section 15.2) which was only
supported on our early machines. The model naturally forms a tree
with the scene represented with increasing spatial resolution as you
go down the different levels of the tree. Goldsmith and Salmon used a
similar strategy to the hierarchical Barnes-Hut approach to particle
dynamics described in Section 12.4. In particular, the upper
parts of the tree are replicated in all nodes and only the lower parts
distributed. This removes ``sequential bottlenecks'' near the top of the tree just as in the astrophysics case.
Originally, Salmon's thesis intended to study the computer science and
science issues associated with hierarchical data structures.
Multiscale methods are pervasive to essentially all
physical systems. However, the success of the astrophysical
applications led to this being his final thesis topic. Su, another
student of Fox, has just finished his Ph.D. on the general mathematical
properties of hierarchical systems [Su:93a].
In Section 14.3, we have a much more irregular and dynamic problem, computer chess, where statistical methods are used to balance the processing of the different branches of the dynamically pruned tree. There is a shared database containing previous evaluation of positions, but otherwise the processing of the different possible moves is independent. One does need a clever ordering of the work (evaluation of the different final positions) to avoid a significant number of calculations being wasted because they would ``later'' be pruned away by a parallel calculation on a different processor. Branch and bound applications [Felten:88c], [Fox:87c;88v] [Fox:87c] have similar parallelization characteristics to computer chess. This was implemented in parallel as a ``best-first'' and not a ``depth-first'' search strategy and was applied to the travelling salesman problem (Section 11.4) to find exact solutions to test the physical optimization algorithms. It was also applied to the 0/1 knapsack problem, but for this and TSP, difficulties arose due to insufficient memory for holding the queues of unexplored subtrees. The depth-first strategy, used in our parallel computer chess program and sequential branch and bound, avoids the need for large memory. On sequential machines, virtual memory can be used for the subtree queues, but this was not implemented on the nCUBE-1 and indeed is absent on most current multicomputers.
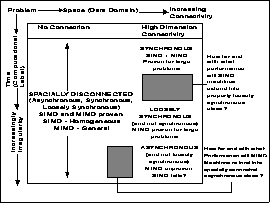
Figure 14.2: Issues Affecting Relation of Machine, Problem, and Software
Architecture
The applications in this chapter are easier than a full event-driven simulation because enough is known about the problem to find a reasonable parallel algorithm. The difficulty then, is to make it efficient. Figure 14.2 is a schematic of problem architectures labelled by spatial and temporal properties. In general, the temporal characteristics-the problem architectures (synchronous, loosely synchronous and asynchronous)-determine the nature of the parallelism. One special case is the spatially disconnected problem class for which the temporal characteristic is essentially irrelevant. For the general spatially connected class, the nature of this connection will affect performance and ease, but not the nature of their parallelism. These issues are summarized in Table 14.4. For instance, spatially irregular problems, such as those in Chapter 12, are particularly hard to implement although they have natural parallelism. The applications in this chapter can be viewed as having little spatial connectivity and their parallelism comes because, although asynchronous, they are ``near'' the spatially disconnected class of Figure 14.2.

Table 14.4: Criterion for success in parallelizing a particular problem
on a particular machine.




