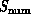 in Equation 3.1), software
(
in Equation 3.1), software
(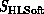 ), and hardware (
), and hardware (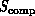 in
Equation 3.1), we will need to further extend this
classification. Here we will briefly define concepts and give the
section number where we discuss and illustrate it more fully.
in
Equation 3.1), we will need to further extend this
classification. Here we will briefly define concepts and give the
section number where we discuss and illustrate it more fully.





As shown in Equation 3.1, we will use complex systems to unify a variety of different concepts including nature and an underlying theory such as Quantum Chromodynamics; the numerical formulation of the theory; the result of expressing this with various software paradigms and the final computer used in its simulation. Different disciplines have correctly been built up around these different complex systems. Correspondingly different terminology is often used to describe related issues. This is certainly reasonable for both historical and technical reasons. However, we argue that understanding the process of computation and answering questions such as, ``Which parallel computers are good for which problems?''; ``What problems parallelize?''; and ``What are productive parallel software paradigms?'' is helped by a terminology which bridges the different complex systems. We can illustrate this with an anecdote. In a recent paper, an illustration of particles in the universe was augmented with a hierarchical set of clusters produced with the algorithm of Section 12.4. These clusters are designed to accurately represent the different length scales and physical clustering of the clouds of particles. This picture was labelled ``data structure'' but one computer science referee noted that this was not appropriate. Indeed, the referee was in one sense correct-we had not displayed a computer science data structure such as a Fortran array or C structure defining the linked list of particles. However, taking the point of view of the physicist, this picture was precisely showing the structure of the data and so, the caption was in one discipline (physics) correct and in another (computer science) false!
We will now define and discuss some general properties and parameters of complex systems which span the various disciplines involved.
We will first discuss possible temporal structures for a complex
system. Here, we draw on a computer science classification of computer
architecture. In this context, aspects such as internode topology
refer to the spatial structure of the computer viewed as a complex
system. The control structure of the computer refers to the temporal
behavior of its complex system. In our review of parallel computer
hardware, we have already introduced the concepts of SIMD and MIMD, two
important temporal classes which carry over to general complex
systems. Returning to Figures 3.7(a) and
3.7(b), we see complex systems which are
MIMD (or asynchronous as defined below) in
Figure 3.7(b) and either SIMD or a restricted form of
MIMD in Figure 3.7(a) (synchronous or loosely synchronous
in language below). In fact, when we consider the temporal structure
of problems (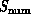 in Equation 3.1), software
(
in Equation 3.1), software
(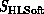 ), and hardware (
), and hardware (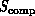 in
Equation 3.1), we will need to further extend this
classification. Here we will briefly define concepts and give the
section number where we discuss and illustrate it more fully.
in
Equation 3.1), we will need to further extend this
classification. Here we will briefly define concepts and give the
section number where we discuss and illustrate it more fully.
Society shows many examples of loosely synchronous behavior. Vehicles proceed more or less independently on a city street between loose synchronization points defined by traffic lights. The reader's life is loosely synchronized by such events as meals and bedtime.
When we consider computer hardware and software systems, we will need to consider other temporal classes which can be thought of as further subdivisions of the asynchronous class.
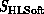 in the notation of Equation 3.1.
One could include shared-memory systems as examples of static
MIMD or dynamic asynchronous systems with a particular form
for information to be transferred between processes or processors. In
distributed-memory machines, information is transferred via the
construction of messages; in shared memory by
memory access instructions. Indeed, the so-called NUMA (non-uniform
memory access) shared-memory machines are implemented in machines like
the Kendall Square as distributed-memory hardware with (from the point
of view of the user) memory access as the communication mechanism.
Uniform memory access (UMA) shared memory machines, such as the
Sequent, do present a rather different computational model. However,
most believe that NUMA machines are the only shared-memory
architectures that scale to large systems, and so in practice scalable
shared-memory architectures are only distinguished from
distributed-memory machines in their mechanism for information
transfer.
in the notation of Equation 3.1.
One could include shared-memory systems as examples of static
MIMD or dynamic asynchronous systems with a particular form
for information to be transferred between processes or processors. In
distributed-memory machines, information is transferred via the
construction of messages; in shared memory by
memory access instructions. Indeed, the so-called NUMA (non-uniform
memory access) shared-memory machines are implemented in machines like
the Kendall Square as distributed-memory hardware with (from the point
of view of the user) memory access as the communication mechanism.
Uniform memory access (UMA) shared memory machines, such as the
Sequent, do present a rather different computational model. However,
most believe that NUMA machines are the only shared-memory
architectures that scale to large systems, and so in practice scalable
shared-memory architectures are only distinguished from
distributed-memory machines in their mechanism for information
transfer.
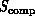 or
or 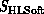 in
Equation 3.1. Here, members of the complex system are
dormant until all data needed for their definition is received when
they ``fire'' and evolve according to a predetermined algorithm.
in
Equation 3.1. Here, members of the complex system are
dormant until all data needed for their definition is received when
they ``fire'' and evolve according to a predetermined algorithm.
In Figure 3.8, we summarize these temporal classifications for complex systems, indicating a partial ordering with arrows pointing to more general architectures. This will become clearer in Section 3.5 when we discuss software and the relation between problem and computer. Note that although the language is drawn from the point of view of computer architecture, the classifications are important at the problem, software, and hardware level.
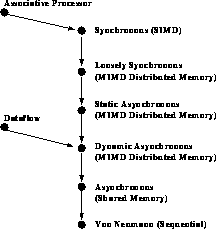
Figure 3.8: Partial Ordering of Temporal (Control) Architectures for a Complex
System
The hardware (computer) architecture naturally divides into SIMD
(synchronous), MIMD (asynchronous), and von Neumann classes. The problem
structures are synchronous, loosely synchronous, or asynchronous. One can
argue that the shared-memory asynchronous architecture is naturally suggested
by software (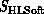 ) considerations and in particular by the goal of
efficient parallel execution for sequential software models. For this reason
it becomes an important computer architecture even though it is not a natural
problem (
) considerations and in particular by the goal of
efficient parallel execution for sequential software models. For this reason
it becomes an important computer architecture even though it is not a natural
problem (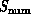 ) architecture.
) architecture.




