


Next: Conclusions and Future Research
Up: OptimizationTuning, and Trade-offs
Previous: Tradeoffs between Load Balance
The communication algorithms used also influence performance. In the LU
factorization algorithm, all the communication can be done by
moving data along rows and/or columns of the process template. This type
of communication can be done by passing from one process to the next
along the row or column. We shall call this a ``ring'' algorithm, although
the ring may, or may not, be closed. An alternative is to use a spanning
tree algorithm, of which there are several varieties. The complexity
of the ring algorithm is linear in the number of processes
involved, whereas that of spanning tree algorithms is logarithmic
(for example, see
[6]). Thus,
considered in isolation, the spanning tree algorithms are preferable to a ring
algorithm. However, in a spanning tree algorithm, a process may take part
in several of the logarithmic steps, and in some implementations these
algorithms act as a barrier. In a ring algorithm, each process needs to
communicate only once, and can then continue to compute, in effect
overlapping the communication with computation. An algorithm that interleaves
communication and calculation in this way is often referred to as a
pipelined algorithm. In a pipelined LU factorization algorithm with no
pivoting, communication and calculation would flow in waves across the matrix.
Pivoting tends to inhibit this advantage of pipelining.
In the pseudocode in Figure 15, we do
not specify how the pivot information
should be broadcast. In an optimized implementation, we
need to finish with the pivot phase, and the triangular solve phase,
as soon as possible in order to begin the update phase which is richest
in parallelism. Thus, it is not a good idea to broadcast the pivot
information from a single source process using a spanning tree algorithm, since
this may occupy some of the processes
involved in
the panel factorization for too long. It is important to get the
pivot information to the other processes in this template column as soon as
possible, so the pivot information is first sent to these processes which
subsequently broadcast it along the template rows to the other
processes not involved in the panel factorization. In addition, the exchange of
the parts of the pivot rows lying within the panel is done separately from
that of the parts outside the pivot panel. Another factor to consider
here is when the pivot information should be broadcast along the template
columns. In Figure 15, the
information is broadcast, and rows exchanged,
immediately after the pivot is found. An alternative is to store up the
sequence of r pivots for a panel and to broadcast them along the
template rows when panel factorization is complete. This defers the exchange
of pivot rows for the parts outside the panel until the panel
factorization has been done, as shown in the pseudocode fragment in
Figure 20. An
advantage of this second approach is that only one message
is used to send the pivot information for the panel along the template
rows, instead of r messages.
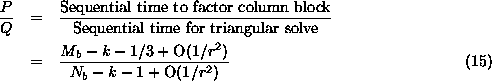
Figure 20: Pseudocode fragment for partial pivoting over rows.
This may be regarded as replacing the first box inside the k loop in
Figure 15.
In the above code pivot information is first disseminated within
the template column doing the panel factorization. The pivoting of the
parts of the rows lying outside the panel is deferred until the panel
factorization has been completed.
In our implementation of LU factorization on the Intel Delta system, we used
a spanning tree algorithm to locate the pivot and to broadcast it within
the column of the process template performing the panel factorization. This
ensures that pivoting, which involves only P processes, is completed as
quickly as possible. A ring broadcast is used to pipeline the pivot
information and the factored panel along the template rows. Finally, after
the triangular solve phase has completed, a spanning
tree broadcast is used to send the newly-formed block row of U along
the template columns. Results for square matrices from runs on the Intel Delta
system are shown
in Figure 21. For each curve the results for the best
process template configuration are shown. For a memory-constrained scalable
algorithm the performance should depend linearly on the number of
processors for fixed granularity, and so
scalability may be assessed by the extent to which isogranularity
curves differ from linearity. An isogranularity curve is a plot of
performance against number of processors for a fixed granularity.
The results in Figure 21 can be used to
generate the isogranularity curves shown in Figure 22 which
show that on the Delta system the LU factorization routine starts to
lose scalability when the granularity falls below about 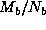 .
This corresponds to a matrix size of about M=10000 on 512 processors, or
about 13% of the memory available to applications on the Delta, indicating
that LU factorization scales rather well on the Intel Delta system.
.
This corresponds to a matrix size of about M=10000 on 512 processors, or
about 13% of the memory available to applications on the Delta, indicating
that LU factorization scales rather well on the Intel Delta system.
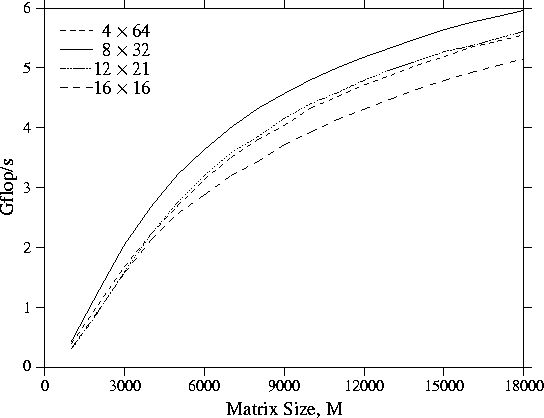
Figure 21: Performance of LU factorization on the Intel Delta as a function
of square matrix size for different numbers of processors. For each curve,
results are shown for the process template configuration that gave the
best performance for that number of processors.
Figure 22: Isogranularity curves in the  plane for the LU factorization
of square matrices on the Intel Delta system. The curves are labeled by the
granularity in units of
plane for the LU factorization
of square matrices on the Intel Delta system. The curves are labeled by the
granularity in units of 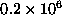 matrix elements per processor. The linearity
of the plots for granularities exceeding about
matrix elements per processor. The linearity
of the plots for granularities exceeding about 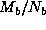 indicates
that the LU factorization algorithm scales well on the Delta.
indicates
that the LU factorization algorithm scales well on the Delta.



Next: Conclusions and Future Research
Up: OptimizationTuning, and Trade-offs
Previous: Tradeoffs between Load Balance
Jack Dongarra
Sun Feb 9 10:05:05 EST 1997
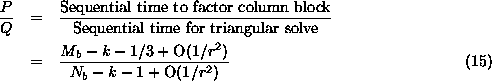

 plane for the LU factorization
of square matrices on the Intel Delta system. The curves are labeled by the
granularity in units of
plane for the LU factorization
of square matrices on the Intel Delta system. The curves are labeled by the
granularity in units of