Use of the PBLAS




Next: Solving Linear Systems
Up: Applications and Use
Previous: Applications and Use
In order to call a PBLAS routine, it is necessary
to initialize the BLACS and create the process grid.
This can be done by calling the routine
BLACS_GRIDINIT (see [14] for more
details). The following segment of code will arrange
four processes into a 2 2
process grid. When running on platforms such as
PVM [20], where the number of computational
nodes available is unknown a priori, it is necessary
to call the routine BLACS_SETUP, so that
copies (3 in our example) of the main program can
be spawned on the virtual machine. Finally, in order
to ensure a safe coexistence with other parallel
libraries using a distinct message passing layer,
such as MPI [17], the BLACS routine
BLACS_GET queries for an eventual system
context (see [14] for more details).
2
process grid. When running on platforms such as
PVM [20], where the number of computational
nodes available is unknown a priori, it is necessary
to call the routine BLACS_SETUP, so that
copies (3 in our example) of the main program can
be spawned on the virtual machine. Finally, in order
to ensure a safe coexistence with other parallel
libraries using a distinct message passing layer,
such as MPI [17], the BLACS routine
BLACS_GET queries for an eventual system
context (see [14] for more details).
INTEGER IAM, ICTXT, NPROCS
*
* (...)
*
CALL BLACS_PINFO( IAM, NPROCS )
*
IF( NPROCS.LT.1 ) THEN
NPROCS = 4
CALL BLACS_SETUP( IAM, NPROCS )
END IF
*
CALL BLACS_GET( -1, 0, ICTXT )
CALL BLACS_GRIDINIT( ICTXT, 'Row-major', 2, 2 )
*
* (...)
*
Moreover, to convey the data distribution information to
the PBLAS, the descriptor of the matrix operands should
be set. The ScaLAPACK library contains a tool routine
called DESCINIT for that purpose. This routine
takes as arguments the 8-integer (descriptor)
array to be initialized, as well as the 8 entries to
be used. Finally, an error flag is set on output to
detect if an incoherent descriptor entry is passed to
this routine. DESCINIT should be called by every
process in the grid.
We present in the following code fragment the descriptor
initialization phase as well as a call to a PBLAS routine.
This sample program performs the matrix multiplication:
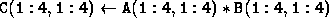 .
.
This example program is to be run on four processes
arranged in a 2 2 process grid.
The matrices
2 process grid.
The matrices 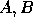 and
and 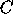 are 5
are 5 5
matrices partitioned into 2
5
matrices partitioned into 2 2 blocks.
We choose the process of coordinates
2 blocks.
We choose the process of coordinates 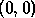 to be the
owner of the first entries of the matrices
to be the
owner of the first entries of the matrices 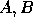 and
and 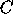 .
The mapping of these matrices is identical to the example
of Fig. 1 given in Sect. 3.2.
.
The mapping of these matrices is identical to the example
of Fig. 1 given in Sect. 3.2.
INTEGER INFO, NMAX, LDA, LDB, LDC, NMAX
PARAMETER ( NMAX = 3, LDA = NMAX, LDB = NMAX, LDC = NMAX )
*
INTEGER DESCA( 8 ), DESCB( 8 ), DESCC( 8 )
DOUBLE PRECISION A( NMAX, NMAX ), B( NMAX, NMAX ), C( NMAX, NMAX )
*
* (...)
*
* Initialize the array descriptors for the matrices A, B and C
*
CALL DESCINIT( DESCA, 5, 5, 2, 2, 0, 0, ICTXT, LDA, INFO )
CALL DESCINIT( DESCB, 5, 5, 2, 2, 0, 0, ICTXT, LDB, INFO )
CALL DESCINIT( DESCC, 5, 5, 2, 2, 0, 0, ICTXT, LDC, INFO )
*
* (...)
*
CALL PDGEMM( 'No transpose', 'No transpose', 4, 4, 4, 1.0D+0,
$ A, 1, 1, DESCA, B, 1, 1, DESCB, 0.0D+0,
$ C, 1, 1, DESCC )
*
* (...)
*
Finally, it is recommended to release the resources
allocated by the BLACS and the PBLAS just before
ending the program segment using the BLACS and the
PBLAS. Note that the routine BLACS_GRIDEXIT
will free the resources associated with a particular
context, while the routine BLACS_EXIT will
free all BLACS resources (see [14] for more
details).
CALL PBFREEBUF()
*
CALL BLACS_GRIDEXIT( ICTXT )
*
CALL BLACS_EXIT( 0 )




Next: Solving Linear Systems
Up: Applications and Use
Previous: Applications and Use
Jack Dongarra
Thu Aug 3 07:53:00 EDT 1995
 2
process grid. When running on platforms such as
PVM [20], where the number of computational
nodes available is unknown a priori, it is necessary
to call the routine BLACS_SETUP, so that
copies (3 in our example) of the main program can
be spawned on the virtual machine. Finally, in order
to ensure a safe coexistence with other parallel
libraries using a distinct message passing layer,
such as MPI [17], the BLACS routine
BLACS_GET queries for an eventual system
context (see [14] for more details).
2
process grid. When running on platforms such as
PVM [20], where the number of computational
nodes available is unknown a priori, it is necessary
to call the routine BLACS_SETUP, so that
copies (3 in our example) of the main program can
be spawned on the virtual machine. Finally, in order
to ensure a safe coexistence with other parallel
libraries using a distinct message passing layer,
such as MPI [17], the BLACS routine
BLACS_GET queries for an eventual system
context (see [14] for more details).
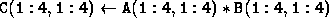 .
.
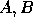 and
and 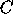 are 5
are 5 to be the
owner of the first entries of the matrices
to be the
owner of the first entries of the matrices