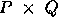Storage Conventions

The current model implementation of the PBLAS assumes the matrix operands to be distributed according to the block-cyclic decomposition scheme. This allows the routines to achieve scalability, well balanced computations and to minimize synchronization costs. It is not the object of this paper to describe in detail the data mapping onto the processes, for further details see [13][7]. Let us simply say that the set of processes is mapped to a virtual mesh, where every process is naturally identified by its coordinates in this 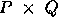grid. This virtual machine is in fact part of a larger object defined by the BLACS and called a context [14].

 
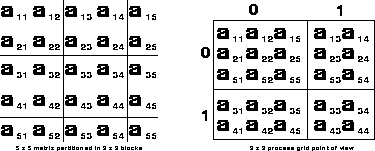
Figure 1: A 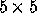matrix decomposed into  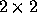 blocks mapped onto a 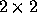process grid.

An M_ by N_ matrix operand is first decomposed into MB_ by NB_ blocks starting at its upper left corner. These blocks are then uniformly distributed across the process mesh. Thus every process owns a collection of blocks, which are locally and contiguously stored in a two dimensional ``column major'' array. We present in Fig. 1 the mapping of a 55 matrix partitioned into 22 blocks mapped onto a 22 process grid, i.e M_=N_=5 and MB_=NB_= 2. The local entries of every matrix column are contiguously stored in the processes' memories.

It follows that a general M_ by N_ distributed matrix is defined by its dimensions, the size of the elementary MB_ by NB_ block used for its decomposition, the coordinates of the process having in its local memory the first matrix entry {RSRC_,CSRC_}, and the BLACS context (CTXT_) in which this matrix is defined. Finally, a local leading dimension LLD_ is associated with the local memory address pointing to the data structure used for the local storage of this distributed matrix. In Fig. 1, we choose for illustration purposes RSRC_=CSRC_=0. In addition, the local arrays in process row 0 must have a leading dimension LLD_ greater than or equal to 3, and greater than or equal to 2 in the process row 1.

These pieces of information are grouped together into a single 8 element integer array, called the descriptor, DESC_. Such a descriptor is associated with each distributed matrix. The entries of the descriptor uniquely determine the mapping of the matrix entries onto the local processes' memories. Moreover, with the exception of the local leading dimension, the descriptor entries are global values characterizing the distributed matrix operand. Since vectors may be seen as a special case of distributed matrices or proper submatrices, the larger scheme just defined encompasses their description as well.

For distributed symmetric and Hermitian matrices, only the upper (UPLO='U') triangle or the lower (UPLO='L') triangle is stored. For triangular distributed matrices, the argument UPLO serves to define whether the matrix is upper (UPLO='U') or lower (UPLO='L') triangular.

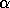For a distributed Hermitian matrix the imaginary parts of the diagonal elements are zero and thus the imaginary parts of the corresponding FORTRAN or C local arrays need not be set, but are assumed to be zero. In the PHER and PHER2 routines, these imaginary parts will be set to zero on return, except when is equal to zero, in which case the routines exit immediately. 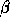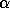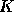Similarly, in the PHERK and PHER2K routines the imaginary parts of the diagonal elements will also be set to zero on return, except when is equal to one and or is equal to zero, in which case the routines exit immediately.