The primary applications of the PBLAS are in implementing algorithms of numerical linear algebra in terms of operations on submatrices (or blocks). Therefore, provisions have been made to easily port sequential programs built on top of the BLAS onto distributed memory computers. Note that the ScaLAPACK library provides a set of tool routines, which the user might find useful for this purpose.
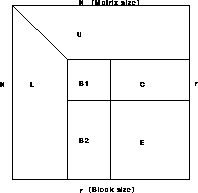
In the following diagram we illustrate how the PBLAS routines can be used to port a simple algorithm of numerical linear algebra, namely solving systems of linear equations via LU factorization. Note that more examples may be found in the ScaLAPACK library.
To obtain a parallel implementation of the LU
factorization of a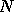 
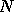-by- matrix, we started
with a variant of the right-looking LAPACK LU
factorization routine given in
appendix B.1.
This algorithm proceeds along the diagonal of
the matrix by first factorizing a block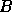 
of
columns at a time, with pivoting if necessary.
Then a triangular solve and a rank- update
are performed on the rest of the matrix. This process
continues recursively with the updated matrix.
For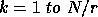 
do
End for;
From the application programmer's point of view, it is conceptually simple to translate the serial version of the code into its parallel equivalent. Translating BLAS calls to PBLAS calls primarily consists of the following steps: a `P' has to be inserted in front of the routine name, the leading dimensions should be replaced by the global array descriptors, and the global indices into the distributed matrices should be inserted as separate parameters in the calling sequence:
CALL DGEMM( 'No transpose', 'No transpose', M-J-JB+1, N-J-JB+1,
$ JB, -ONE, A( J+JB, J ), LDA, A( J, J+JB ), LDA, ONE,
$ A( J+JB, J+JB ), LDA )
CALL PDGEMM( 'No transpose', 'No transpose', M-J-JB+JA, N-J-JB+JA,
$ JB, -ONE, A, I+JB, J, DESCA, A, I, J+JB, DESCA, ONE,
$ A, I+JB, J+JB, DESCA )
This simple translation process considerably simplifies the implementing phase of linear algebra codes built on top of the BLAS. Moreover, the global view of the matrix operands allows the user to be concerned only with the numerical details of the algorithms and a minimum number of important details necessary to programs written for distributed-memory computers.
The resulting parallel code is given in appendix B along with the serial code. These codes are very similar as most of the details of the parallel implementation such as communication and synchronization have been hidden at lower levels of the software.
In addition, the underlying block-cyclic decomposition scheme ensures good load-balance, and thus performance and scalability. In the particular example of the LU factorization, it is possible to take advantage of other parallel algorithmic techniques such as pipelining and the overlapping of computation and communication operations. Because the factorization and pivoting phases of the algorithm described above are much less computational intensive than its update phase, it is intuitively suitable to communicate the pivot indices as soon as possible to all processes in the grid, especially to those who possess the next block of columns to be factorized. In this way the update phase can be started as early as possible [13]. Such a pipelining effect can easily be achieved within PBLAS based codes by using ring topologies along process rows for the broadcast operations. These particular algorithmic techniques are enabled by the PBLAS auxiliary routines PTOPGET and PTOPSET (see Sect. 5.1.2). They notably improve the performance and the scalability of the parallel implementation.