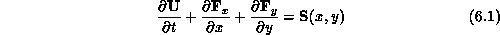
The governing equations are similar to those in Section 12.3.1, namely, the two-dimensional Euler equations,
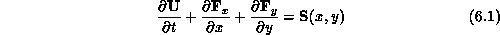
where,
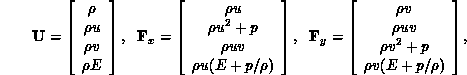
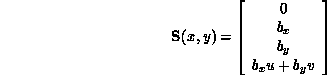
Here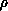 
is the fluid mass density, E is the specific energy, u and v
are the fluid velocities in the x and y directions, 
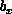and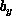 
are body force components, and the pressure, p, is given by,
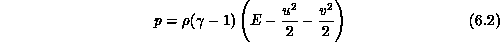
where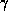 
is the constant adiabatic index. The motion of the fluid
is tracked by introducing massless marker particles and allowing them to be
advected with the flow. Thus, the number density of the marker particles,
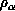, satisfies,
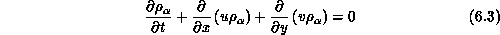
The equations are solved on a rectilinear two-dimensional grid. Second-order accuracy in time is maintained by first advancing the velocities by a half time step, and then using these velocities to update all values for the full time step. The size of the time step is governed by the Courant condition.
The basic procedure in each time step is to first apply a five-point difference operator at each grid point to convectively transport the field values. These field values are then diffused in each of the positive and negative x and y directions. The behavior of the resulting fields in the vicinity of each grid point is then examined to determine how much diffusion to remove at that point. In regions where a field value is locally monotonic, nearly all the diffusion previously applied is removed for that field. However, in regions close to extrema, the amount of diffusion removed is less.