12.3.1 Compressible Flow Algorithm

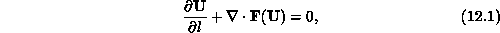
The governing equations are the Euler equations, which are of advective type with no diffusion,

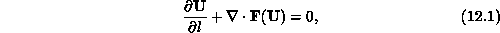
where U is a vector containing the information about the fluid at a point. I have used bold symbols to indicate an information vector, or a set of fields describing the state of the fluid. In this implementation, U consists of density, velocity, and specific total energy (or, equivalently, pressure); it could also include other information about the state of the fluid such as chemical mixture or ionization data. F is the flux vector and has the same structure as U in each of the two coordinate directions.

The numerical algorithm is explained in detail in [Mavriplis:88a], so only an outline is given here. The method uses linear triangular elements to approximate the field. First, a time step is chosen for each node which is constrained by a local Courant condition. The calculation consists of two parts:

Advection: At each node, calculate F from U. Each element then averages F from its neighboring nodes, and calculates the flux across each edge of the element, which is then added back into the node opposite the edge. This change in U is combined across the representations of the node in different processors. If the node is at a boundary which is a hard surface, a modification is made so that no flux of mass or energy occurs through the surface.

Artificial Dissipation: The artificial dissipation is calculated as a combination of approximations to the Laplacian and the double Laplacian of U, involving a combine step for each. The double Laplacian is only used where the flow is smooth, to prevent dissipation of strong shocks.

The time stepping is done with a five-stage Runge-Kutta scheme, where the advection step is done five times, and the dissipation step is done twice. Since advection takes one communication stage and dissipation two, each full time step requires nine loosely synchronous communication stages.