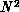Unstructured meshes have been widely used for calculations with conventional sequential machines. Jameson [Jameson:86a;86b] uses explicit finite-element-based schemes on fully unstructured tetrahedral meshes to solve for the flow around a complete aircraft, and other workers [Dannenhoffer:89a], [Holmes:86a], [Lohner:84a;85a;86a] have used unstructured triangular meshes. Jameson and others [Jameson:87a;87b], [Mavriplis:88a], [Perez:86a], [Usab:83a] have used multigrid methods to accelerate convergence . For this work [Williams:89b], we have used the two-dimensional explicit algorithm of Jameson and Mavriplis [Mavriplis:88a].
An explicit update procedure is local, and hence well matched to a massively
parallel distributed machine, whereas an implicit algorithm is more difficult
to parallelize. The implicit step consists of solving a sparse set of linear
equations, where matrix elements are nonzero only for mesh-connected nodes.
Matrix multiplication is easy to parallelize since it is also a local
operation, and the solve may thus be accomplished by an iterative technique
such as conjugate gradient, which consists of repeated matrix
multiplications. If, however, the same solve is to be done repeatedly for
the same mesh, the most efficient (sequential) method is first decomposing
the matrix in some way, resulting in fill-in. In terms of the mesh, this
fill-in represents nonlocal connection between nodes:indeed, if the
matrix were completely filled, the communication time would be proportional to
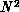for N nodes.