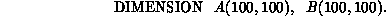





In Section 3.3, we noted that the concept of space and time are not preserved in the mappings between complex systems defined in Equation 3.1. We can use this to motivate some advantage in using the array notation used in Fortran 90. Consider a complex problem whose data domain is expressed in two Fortran arrays A and B with, say,
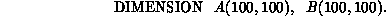
Suppose some part of the program involves adding the arrays, which is expressed as
in Fortran 90 and
in Fortran 77. In this last equation, the data-parallel spatial manipulation of Equation 13.1 is converted into 10,000 time steps. In other words, Fortran 77 has not preserved the spatial structure of the problem. The task of a parallelizing Fortran 77 compiler is to reverse this procedure by recognizing that the sequential (time-stepped) DO loops are ``just'' a spatially (data)-parallel expression. We find mappings:
Note that the final parallel computer implementation maps the original spatial structure into a combination of time (the ``node'' program) and space (distribution) over nodes.
We can attribute some of the difficulties in producing an effective Fortran 77 compiler to the unfortunate mapping of space into time (control) shown in Equation 13.4. In the trivial example of Equation 13.3, one can undo this ``wrong,'' but in general there is not enough compile time information in a Fortran 77 code to recover the original spatial parallelism. In this language, Fortran-plus message passing also does not preserve the spatial structure, but rather maps into a mix of space (the message-passing parallelism) and time (node Fortran).