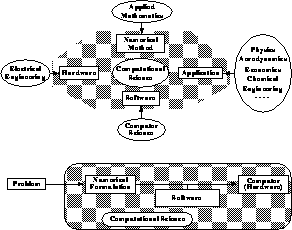
Figure 3.3: An Interdisciplinary Approach to Computing with Computational Science Shown Shaded





There is no agreed-upon process behind computation, that is, behind the use of a computer to solve a particular problem. We have tried to quantify this in Figures 3.1(b), 3.2(b), and 3.3 which show a problem being first numerically formulated and then mapped by software onto a computer.

Figure 3.3: An Interdisciplinary Approach to Computing with Computational
Science Shown Shaded
Even if we could get agreement on such an ``underlying'' process, the definitions of the parts of the process are not precise and correspondingly the roles of the ``experts'' are poorly defined. This underlies much of the controversy, and in particular, why we cannot at present or probably ever be able to define ``The best software methodology for parallel computing.''
How can we agree on a solution (What is the appropriate software?) unless we can agree on the task it solves?
``What is computation and how can it be broken up into components?''In other words, what is the underlying process?
In spite of our pessimism that there is any clean, precise answer to this question, progress can be made with an imperfect process defined for computation. In the earlier figures, it was stressed that software could be viewed as mapping problems onto computers. We can elaborate this as shown in Figure 3.4, with the solution to a question pictured as a sequence of idealizations or simplifications which are finally mapped onto the computer. This process is spelled out for four examples in Figures 3.5 and 3.6. In each case, we have tried to indicate possible labels for components of the process. However, this can only be approximate. We are not aware of an accepted definition for the theoretical or computational parts of the process. Again, which parts are modelling or simulation? Further, there is only an approximate division of responsibility among the various ``experts''; for example, between the theoretical physicist and the computational physicist, or among aerodynamics, applied mathematics, and computer science. We have also not illustrated that, in each case, the numerical algorithm is dependent on the final computer architecture targeted; in particular, the best parallel algorithm is often different from the best conventional sequential algorithm.
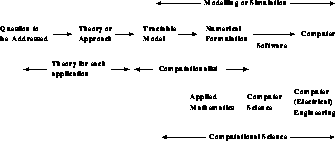
Figure 3.4: An Idealized Process of Computation
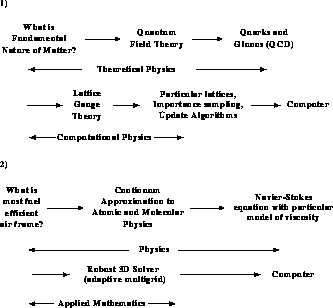
Figure 3.5: A Process for Computation in Two Examples in Basic Physics
Simulations
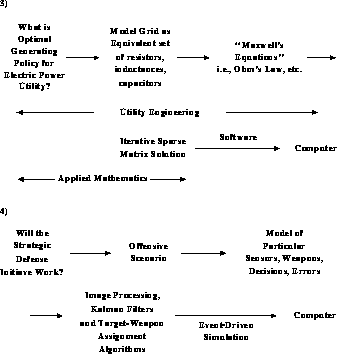
Figure 3.6: A Process for Computation in Two Examples from Large Scale
System Simulations
We can abstract Figures 3.5 and 3.6 into a sequence
of maps between complex systems 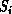 ,
, 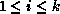 .
.
We have anticipated (Chapter 5) and broken the software into a high level component (such as a compiler) and a lower level one (such as an assembler) which maps a ``virtual computer'' into the particular machine under consideration. In fact, the software could have more stages, but two is the most common case for simple (sequential) computers.
A complex system, as used here, is defined as a collection of fundamental
entities whose static or dynamic properties define a connection scheme
between the entities. Complex systems have a structure or architecture.
For instance, a binary hypercube parallel computer of dimension d is
a complex system with 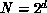 members connected in a hypercube
topology. We can focus in on the node of the hypercube and expand the
node, viewed itself as a complex system, into a collection of memory
hierarchies, caches, registers, CPU., and communication channels. Even
here, we find another ill-defined point with the complex system representing
the computer dependent on the resolution or granularity with which you
view the system. The importance of the architecture of a computer
system
members connected in a hypercube
topology. We can focus in on the node of the hypercube and expand the
node, viewed itself as a complex system, into a collection of memory
hierarchies, caches, registers, CPU., and communication channels. Even
here, we find another ill-defined point with the complex system representing
the computer dependent on the resolution or granularity with which you
view the system. The importance of the architecture of a computer
system  has been recognized for many years. We suggest
that the architecture or structure of the problem is comparably
interesting. Later, we will find that the performance of a particular
problem or machine can be studied in terms of the match (similarity)
between the architectures of the complex systems
has been recognized for many years. We suggest
that the architecture or structure of the problem is comparably
interesting. Later, we will find that the performance of a particular
problem or machine can be studied in terms of the match (similarity)
between the architectures of the complex systems 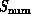 and
and
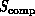 defined in Equation 3.1. We will find
that the structure of the appropriate parallel software will depend on
the broad features of the (similar) architecture of
defined in Equation 3.1. We will find
that the structure of the appropriate parallel software will depend on
the broad features of the (similar) architecture of 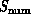 and
and
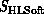 . This can be expected as software maps the two
complex systems into each other.
. This can be expected as software maps the two
complex systems into each other.
At times, we have talked in terms of problem architecture, but this is ambiguous since it could refer to any of the
complex systems 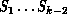 which can and usually do have
different architectures. Consider the second example of
Figure 3.5 with the computational fluid
dynamics study of airflow. In the
language of Equation 3.1:
which can and usually do have
different architectures. Consider the second example of
Figure 3.5 with the computational fluid
dynamics study of airflow. In the
language of Equation 3.1:
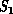 is a (finite) collection of molecules interacting with
long-range Van der Waals and other forces. This interaction defines a
complete interconnect between all members of the complex system
is a (finite) collection of molecules interacting with
long-range Van der Waals and other forces. This interaction defines a
complete interconnect between all members of the complex system 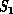 .
.
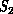 is the infinite degree of freedom continuum with the fundamental
entities as infinitesimal volumes of air connected locally by the partial
differential operator of the Navier Stokes equation.
is the infinite degree of freedom continuum with the fundamental
entities as infinitesimal volumes of air connected locally by the partial
differential operator of the Navier Stokes equation.
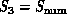 could depend on the particular numerical
formulation used. Multigrid, conjugate gradient , direct matrix inversion and alternating gradient would have
very different structures in the direct numerical solution of the
Navier Stokes equations. The more radical cellular
automata approach would be quite different
again.
could depend on the particular numerical
formulation used. Multigrid, conjugate gradient , direct matrix inversion and alternating gradient would have
very different structures in the direct numerical solution of the
Navier Stokes equations. The more radical cellular
automata approach would be quite different
again.
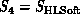 would depend on the final computer being used
and division between high and low level in software. In the applications
described in this book,
would depend on the final computer being used
and division between high and low level in software. In the applications
described in this book, 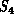 would typically be a simple binary hypercube
with
would typically be a simple binary hypercube
with 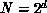 nodes.
nodes.
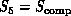 would be
would be 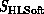 embroidered by the
details of the hardware communication (circuit or packet switching, wormhole
or other routing). Further, as described above, in some analyses we could
look at this complex system in greater resolution and expose the details of
the processor node architecture.
embroidered by the
details of the hardware communication (circuit or packet switching, wormhole
or other routing). Further, as described above, in some analyses we could
look at this complex system in greater resolution and expose the details of
the processor node architecture.




