




Next: 4.2 Synchronous Applications
Up: 4 Synchronous Applications I
Previous: 4 Synchronous Applications I
The Caltech Concurrent Computation Project started with QCD, or
Quantum Chromodynamics, as its first
application. QCD is discussed in more detail in Sections 4.2 and
4.3, but here we will put in the historical perspective.
This nostalgic approach is developed in [Fox:87d], [Fox:88oo]
as well as Chapters 1 and 2 of this book.
We show, in Table 4.1, fourteen QCD simulations, labelled by
representative physics publications, performed within C P using
parallel machines. This activity started in 1981 with simulations,
using the first four-node 8086-8087-based prototypes of the Cosmic
Cube. These prototypes were quite competitive in performance with the
VAX 11/780 on which we had started (in 1980) our computational physics
program within high energy physics at
Caltech. The 64-node Cosmic Cube was used more or
less continuously from October, 1983 to mid-1984 on what was termed by
Caltech, a ``mammoth calculation'' in the press release shown in
Figure 4.2. This is the modest,
P using
parallel machines. This activity started in 1981 with simulations,
using the first four-node 8086-8087-based prototypes of the Cosmic
Cube. These prototypes were quite competitive in performance with the
VAX 11/780 on which we had started (in 1980) our computational physics
program within high energy physics at
Caltech. The 64-node Cosmic Cube was used more or
less continuously from October, 1983 to mid-1984 on what was termed by
Caltech, a ``mammoth calculation'' in the press release shown in
Figure 4.2. This is the modest, 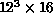 four-dimensional lattice calculation reported in line 3 of
Table 4.1. As trumpeted in Figures 4.1 and
4.2, this was our first major use of parallel machines and
a critical success on which we built our program.
four-dimensional lattice calculation reported in line 3 of
Table 4.1. As trumpeted in Figures 4.1 and
4.2, this was our first major use of parallel machines and
a critical success on which we built our program.
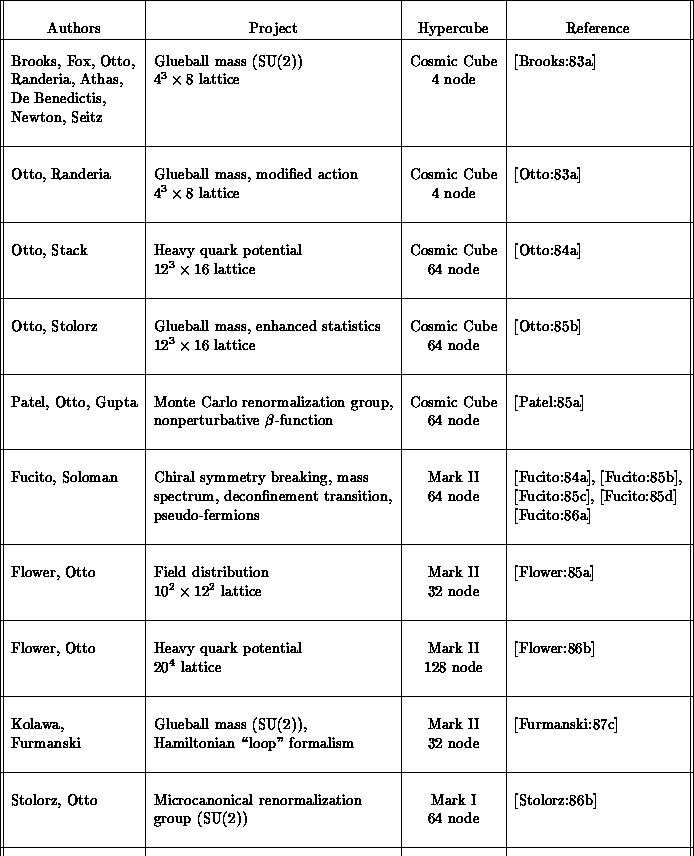
Table 4.1: Quantum Chromodynamic (QCD) Calculations Within C P
P
Our 1983-1984 calculations totalled some 2,500 hours on the 64-node
Cosmic Cube and successfully competed with 100-hour CDC
Cyber 205 computations that were the state of the art at the time
[Barkai:84b], [Barkai:84c], [Bowler:85a],
[DeForcrand:85a]. We used a four-dimensional lattice with 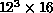 grid points, with eight gluon field values defined on each
of the 110,592 links between grid points. The resultant 884,736
degrees of freedom seem modest today as QCD practitioners contemplate
lattices of order
grid points, with eight gluon field values defined on each
of the 110,592 links between grid points. The resultant 884,736
degrees of freedom seem modest today as QCD practitioners contemplate
lattices of order 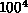 simulated on machines of
teraFLOP performance [Aoki:91a]. However, this
lattice was comparable to those used on vector supercomputers at the
time.
simulated on machines of
teraFLOP performance [Aoki:91a]. However, this
lattice was comparable to those used on vector supercomputers at the
time.
A hallmark of this work was the interdisciplinary team building hardware,
software, and parallel application. Further, from the start we stressed
large supercomputer-level simulations where parallelism would make the
greatest initial impact. It was also worth noting that our use of
comparatively high-level software paid off-Otto and Stack were able to
code better algorithms [Parisi:83a] than the competing vector
supercomputer teams. The hypercube could be programmed conveniently
without use of microcode or other unproductive environments needed on
some of the other high-performance machines of the time.
Our hypercube calculations used an early C plus message-passing
programming approach which later evolved into the Express system
described in the next chapter. Although not as elegant as data-parallel
C and Fortran (discussed in Chapter 13), our approach was easier
than hand-coded assembly, which was quite common for alternative
high-performance systems of the time.
Figures 4.1 and 4.2 show extracts from
Caltech and newspaper publicity of the time. We were essentially only
a collection of 64 IBM PCs. Was that a good thing (as we thought) or
an indication of our triviality (as a skeptical observer commenting in
Figure 4.1 thought)? 1985 saw the start of a new phase as
conventional supercomputers and availability increased in power and NSF
and DOE allocated many tens of thousands of hours on the
CRAY X-MP (2, Y-MP) and ETA-10 to QCD simulations. Our
final QCD hypercube calculations in 1989 within C P used a 64-node
JPL Mark IIIfp with approximately
P used a 64-node
JPL Mark IIIfp with approximately 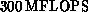 performance. Since
this work, we switched to using the Connection Machine CM-2, which by 1990 was the commercial standard in the field.
C
performance. Since
this work, we switched to using the Connection Machine CM-2, which by 1990 was the commercial standard in the field.
C P helped the Los Alamos group of Brickner and Gupta (one of our
early graduates!) to develop the first CM-2 QCD codes, which in 1991
performed at
P helped the Los Alamos group of Brickner and Gupta (one of our
early graduates!) to develop the first CM-2 QCD codes, which in 1991
performed at 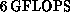 on the full size
on the full size 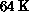 CM-2
[Brickner:91a], [Liu:91a].
CM-2
[Brickner:91a], [Liu:91a].
Caltech Scientists Develop `Parallel' Computer Model
By LEE DEMBART
Times Science Writer
Caltech scientists have developed a working prototype for a new super
computer that can perform many tasks at once, making possible the
solution of important science and engineering problems that have so
far resisted attack.
The machine is one of the first to make extensive use of parallel
processing, which has been both the dream and the bane of computer
designers for years.
Unlike conventional computers, which perform one step at a time while
the rest of the machine lies idle, parallel computers can do many
things at the same time, holding out the prospect of much greater
computing speed than currently available-at much less cost.
If its designers are right, their experimental device, called the
Cosmic Cube, will open the way for solving problems in
meteorology, aerodynamics,
high-energy physics, seismic analysis,
astrophysics and oil exploration, to name a few.
These problems have been intractable because even the fastest of
today's computers are too slow to process the mountains of data in a
reasonable amount of time.
One of today's fastest computers is the Cray 1, which can do 20
million to 80 million operations a second. But at $5 million, they
are expensive and few scientists have the resources to tie one up
for days or weeks to solve a problem.
``Science and engineering are held up by the lack of super
computers,'' says one of the Caltech inventors, Geoffrey C. Fox, a
theoretical physicist. ``They know how to solve problems that are
larger than current computers allow.''
The experimental device, 5 feet long by 8 inches high by 14 inches
deep, fits on a desk top in a basement laboratory, but it is already
the most powerful computer at Caltech. It cost $80,000 and can do
three million operations a second-about one-tenth the power of a
Cray 1.
Fox and his colleague, Charles L. Seitz, a computer scientist, say
they can expand their device in coming years so that it has 1,000
times the computing power of a Cray.
``Poor old Cray and Cyber (another super computer) don't have much of
a chance of getting any significant increase in speed,'' Fox said.
``Our ultimate machines are expected to be at least 1,000 times faster
than the current fastest computers.''
``We are getting to the point where we are not going to be talking
about these things as fractions of a Cray but as multiples of them,''
Seitz said.
But not everyone in the field is as impressed with Caltech's Cosmic
Cube as its inventors are. The machine is nothing more nor less than
64 standard, off-the-shelf microprocessors wired together, not much
different than the innards of 64 IBM personal computers working as a
unit.
``We are using the same technology used in PCs (personal computers)
and Pacmans,'' Seitz said. The technology is an 8086 microprocessor
capable of doing 1/20th of a million operations a second with 1/8th of
a megabyte of primary storage. Sixty-four of them together will do 3
million operations a second with 8 megabytes of storage.
Currently under development is a single chip that will replace each of
the 64 8-inch-by-14-inch boards. When the chip is ready, Seitz and
Fox say they will be able to string together 10,000 or even 100,000 of
them.
Computer scientists have known how to make such a computer for years
but have thought it too pedestrian to bother with.
``It could have been done many years ago,'' said Jack B. Dennis, a
computer scientist at the Massachusetts Institute of Technology who is
working on a more radical and ambitious approach to parallel
processing than Seitz and Fox. He thinks his approach, called
``dataflow,'' will both speed up computers and expand
their horizons, particularly in the direction of artificial
intelligence .
Computer scientists dream of getting parallel processors to mimic the
human brain , which can also do things concurrently.
``There's nothing particularly difficult about putting together 64 of
these processors,'' he said. ``But many people don't see that sort of
machine as on the path to a profitable result.''
What's more, Dennis says, organizing these machines and writing
programs for them have turned out to be sticky problems that have
resisted solution and divided the experts.
``There is considerable debate as to exactly how these large parallel
machines should be programmed,'' Dennis said by telephone from
Cambridge, Mass. ``The 64-processor machine (at Caltech) is, in terms
of cost-performance, far superior to what exists in a Cray 1 or a
Cyber 205 or whatever. The problem is in the programming.''
Fox responds that he has ``an existence proof'' for his machine and
its programs, which is more than Dennis and his colleagues have to
show for their efforts.
The Caltech device is a real, working computer, up and running and
chewing on a real problem in high-energy physics. The ideas on which
it was built may have been around for a while, he agreed, but the
Caltech experiment demonstrates that there is something to be gained
by implementing them.
For all his hopes, Dennis and his colleagues have not yet built a
machine to their specifications. Others who have built parallel
computers have done so on a more modest scale than Caltech's 64
processors. A spokesman for IBM said that the giant computer company
had built a 16-processor machine, and is continuing to explore
parallel processing.
The key insight that made the development of the Caltech computer
possible, Fox said, was that many problems in science are
computationally difficult because they are big, not because they are
necessarily complex.
Because these problems are so large, they can profitably be divided
into 64 parts. Each of the processors in the Caltech machine works on
1/64th of the problem.
Scientists studying the evolution of the universe have to deal with 1
million galaxies. Scientists studying aerodynamics get
information from thousands of data points in three dimensions.
To hunt for undersea oil, ships tow instruments through the oceans,
gathering data in three dimensions that is then analyzed in two
dimensions because of computer limitations. The Caltech computer
would permit three-dimensional analysis.
``It has to be problems with a lot of concurrency in them,'' Seitz
said. That is, the problem has to be split into parts, and all the
parts have to be analyzed simultaneously.
So the applications of the Caltech computer for commercial uses such
as an airline reservation system would be limited, its inventors
agree.

Figure 4.1: Caltech Scientists Develop ``Parallel'' Computer Model
[Dembart:84a]
CALTECH'S COSMIC CUBE
PERFORMING MAMMOTH CALCULATIONS
Large-scale calculations in basic physics have been successfully run
on the Cosmic Cube, an experimental computer at Caltech that its
developers and users see as the forerunner of supercomputers of the
future. The calculations, whose results are now being published in
articles in scientific journals, show that such computers can deliver
useful computing power at a far lower cost than today's machines.
The first of the calculations was reported in two articles in the June
25 issue of  . In addition,
a second set of calculations related to the first has been submitted
to
. In addition,
a second set of calculations related to the first has been submitted
to 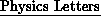 for publication.
for publication.
The June 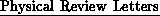 articles were:
articles were:
-``Pure Gauge SU(3) Lattice Theory on an Array of Computers,'' by
Eugene Brooks, Geoffrey Fox, Steve Otto, Paul Stolorz, William Athas,
Erik DeBenedictis, Reese Faucette, and Charles Seitz, all of
Caltech; and John Stack of the University of Illinois at
Urbana-Champaign, and
-``The SU(3) Heavy Quark Potential with High Statistics,'' by Steve
Otto and John Stack.
The Cosmic Cube consists of 64 computer elements, called nodes, that
operate on parts of a problem concurrently. In contrast, most
computers today are so-called von Neumann machines, consisting of a
single processor that operates on a problem sequentially, making
calculations serially.
The calculation reported in the June 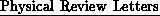 took 2,500 hours of the computation time on the
Cosmic Cube. The calculation represents a contribution to the test of
a set of theories called the Quantum Field Theories, which are
mathematical attempts to explain the physical properties of subatomic
particles known as hadrons, which include protons and neutrons.
took 2,500 hours of the computation time on the
Cosmic Cube. The calculation represents a contribution to the test of
a set of theories called the Quantum Field Theories, which are
mathematical attempts to explain the physical properties of subatomic
particles known as hadrons, which include protons and neutrons.
These basic theories represent in a series of equations the behavior
of quarks, the basic constituents of hadrons. Although theorists
believe these equations to be valid, they have never been directly
tested by comparing their predictions with the known properties of
subatomic particles as observed in experiments with particle
accelerators.
The calculations to be published in 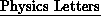 probe the properties, such as mass, of the glueballs that are
predicted by theory.
probe the properties, such as mass, of the glueballs that are
predicted by theory.
``The calculations we are reporting are not earth-shaking,'' said Dr.
Fox. ``While they are the best of their type yet done, they represent
but a steppingstone to better calculations of this type.'' According
to Dr. Fox, the scientists calculated the force that exists between
two quarks. This force is carried by gluons, the particles that are
theorized to carry the strong force between quarks. The aim of the
calculation was to determine how the attractive force between quarks
varies with distance. Their results showed that the potential depends
linearly on distance.
``These results indicate that it would take an infinite amount of
energy to separate two quarks, which shows why free quarks are not
seen in nature,'' said Dr. Fox. ``These findings represent a
verification of what most people expected.''
The Cosmic Cube has about one-tenth the power of the most widely used
supercomputer, the Cray-1, but at one hundredth the cost, about
$80,000. It has about eight times the computing power of the widely
used minicomputer, the VAX 11/780. Physically, the machine occupies
about six cubic feet, making it fit on the average desk, and uses 700
watts of power.
Each of the 64 nodes of the Cosmic Cube has approximately the same
power as a typical microcomputer, consisting of 16-bit Intel 8086 and
8087 processors, with 136K bytes of memory storage. For comparison,
the IBM Personal Computer uses the same family of chips and typically
possesses a similar amount of memory. Each of the Cosmic Cube nodes
executes programs concurrently, and each can send messages to six
other nodes in a communication network based on a six-dimensional
cube, or hypercube. The chips for the Cosmic Cube were donated by
Intel Corporation, and Digital Equipment Corporation contributed
supporting computer hardware. According to Dr. Fox, a full-scale
extension of the Quantum Field Theories to yield the properties of
hadrons would require a computer 1,000 times more powerful than the
Cosmic Cube-or 100 computer projects at Caltech are developing
hardware and software for such advanced machines.

Figure 4.2: Caltech's Cosmic Cube Performing Mammoth Calculations
[Meredith:84a]
It is not surprising that our first hypercube calculations in C P did
not need the full MIMD structure of the machine. This was also a
characteristic of Sandia's pioneering use of the 1024-node nCUBE-[Gustafson:88a]. Synchronous applications like QCD are
computationally important and have a simplicity that made them the
natural starting point for our project.
P did
not need the full MIMD structure of the machine. This was also a
characteristic of Sandia's pioneering use of the 1024-node nCUBE-[Gustafson:88a]. Synchronous applications like QCD are
computationally important and have a simplicity that made them the
natural starting point for our project.





Next: 4.2 Synchronous Applications
Up: 4 Synchronous Applications I
Previous: 4 Synchronous Applications I
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
 P using
parallel machines. This activity started in 1981 with simulations,
using the first four-node 8086-8087-based prototypes of the Cosmic
Cube. These prototypes were quite competitive in performance with the
VAX 11/780 on which we had started (in 1980) our computational physics
program within high energy physics at
Caltech. The 64-node Cosmic Cube was used more or
less continuously from October, 1983 to mid-1984 on what was termed by
Caltech, a ``mammoth calculation'' in the press release shown in
Figure 4.2. This is the modest,
P using
parallel machines. This activity started in 1981 with simulations,
using the first four-node 8086-8087-based prototypes of the Cosmic
Cube. These prototypes were quite competitive in performance with the
VAX 11/780 on which we had started (in 1980) our computational physics
program within high energy physics at
Caltech. The 64-node Cosmic Cube was used more or
less continuously from October, 1983 to mid-1984 on what was termed by
Caltech, a ``mammoth calculation'' in the press release shown in
Figure 4.2. This is the modest, 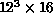 four-dimensional lattice calculation reported in line 3 of
Table 4.1. As trumpeted in Figures 4.1 and
4.2, this was our first major use of parallel machines and
a critical success on which we built our program.
four-dimensional lattice calculation reported in line 3 of
Table 4.1. As trumpeted in Figures 4.1 and
4.2, this was our first major use of parallel machines and
a critical success on which we built our program.






 P
P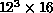 grid points, with eight gluon field values defined on each
of the 110,592 links between grid points. The resultant 884,736
degrees of freedom seem modest today as QCD practitioners contemplate
lattices of order
grid points, with eight gluon field values defined on each
of the 110,592 links between grid points. The resultant 884,736
degrees of freedom seem modest today as QCD practitioners contemplate
lattices of order 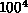 simulated on machines of
teraFLOP
simulated on machines of
teraFLOP P used a 64-node
JPL Mark IIIfp with approximately
P used a 64-node
JPL Mark IIIfp with approximately 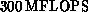 performance. Since
this work, we switched to using the Connection Machine
performance. Since
this work, we switched to using the Connection Machine P helped the Los Alamos group of Brickner and Gupta (one of our
early graduates!) to develop the first CM-2 QCD codes, which in 1991
performed at
P helped the Los Alamos group of Brickner and Gupta (one of our
early graduates!) to develop the first CM-2 QCD codes, which in 1991
performed at 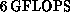 on the full size
on the full size 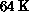 CM-2
[
CM-2
[
 . In addition,
a second set of calculations related to the first has been submitted
to
. In addition,
a second set of calculations related to the first has been submitted
to  for publication.
for publication.
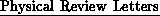 articles were:
articles were:
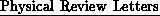 took 2,500 hours of the computation time on the
Cosmic Cube. The calculation represents a contribution to the test of
a set of theories called the Quantum Field Theories, which are
mathematical attempts to explain the physical properties of subatomic
particles known as hadrons, which include protons and neutrons.
took 2,500 hours of the computation time on the
Cosmic Cube. The calculation represents a contribution to the test of
a set of theories called the Quantum Field Theories, which are
mathematical attempts to explain the physical properties of subatomic
particles known as hadrons, which include protons and neutrons.
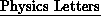 probe the properties, such as mass, of the glueballs that are
predicted by theory.
probe the properties, such as mass, of the glueballs that are
predicted by theory.

 P did
not need the full MIMD structure of the machine. This was also a
characteristic of Sandia's pioneering use of the 1024-node nCUBE-[
P did
not need the full MIMD structure of the machine. This was also a
characteristic of Sandia's pioneering use of the 1024-node nCUBE-[