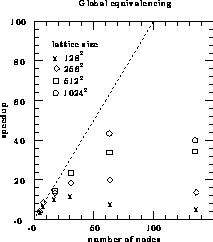
Figure 12.28: Speedups for Global Equivalencing Algorithm





In this method we again use the fastest sequential algorithm to identify the clusters in the sublattice on every processor. Each processor then looks at the labels of sites along the edges of the neighboring processors in the positive directions, and works out which ones are connected and should be matched up. These lists of ``equivalences'' are all passed to one of the processors, which uses an algorithm for finding equivalence classes [Knuth:68a], [Press:86a] (which, in this case, are the global cluster labels) to match up the connected clusters. This processor then broadcasts the results back to all the other processors.

Figure 12.28: Speedups for Global Equivalencing Algorithm
This part of the algorithm is purely sequential, and is thus a potentially
disastrous bottleneck for large numbers of processors. It also requires
this processor to have a large amount of memory in which to store all the
labels from every other processor. The amount of work involved in doing the
global matchup is proportional to P times the perimeter of the
sublattice on each processor, or 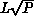 so that the efficiency
should be less than for self-labelling; although, we might still
expect reasonable speedups if the number of processors is not extremely
large. The speedups obtained on the Symult 2010 for a variety of
lattice sizes are shown in Figure 12.28. The figure for
so that the efficiency
should be less than for self-labelling; although, we might still
expect reasonable speedups if the number of processors is not extremely
large. The speedups obtained on the Symult 2010 for a variety of
lattice sizes are shown in Figure 12.28. The figure for
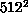 on 128 processors is missing due to memory constraints. Global
equivalencing gives about the same speedups as self-labelling for small
numbers of processors, but as expected self-labelling
does much better as the number of processors increases.
on 128 processors is missing due to memory constraints. Global
equivalencing gives about the same speedups as self-labelling for small
numbers of processors, but as expected self-labelling
does much better as the number of processors increases.