




Next: 12.6.5 Global Equivalencing
Up: 12.6 Cluster Algorithms for
Previous: 12.6.3 Parallel Cluster Algorithms
We shall refer to this algorithm as ``self-labelling,'' since each site
figures out which cluster it is in by itself from local information.
This method has also been referred to as ``local label propagation''
[Brower:91a], [Flanigan:92a].
We begin by assigning each site, i, a unique cluster label, 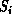 . In
practice, this is simply chosen as the position of that site in the lattice.
At each step of the algorithm in parallel, every site looks in turn at each
of its neighbors in the positive directions. If it is bonded to a
neighboring site, n, which has a different cluster label,
. In
practice, this is simply chosen as the position of that site in the lattice.
At each step of the algorithm in parallel, every site looks in turn at each
of its neighbors in the positive directions. If it is bonded to a
neighboring site, n, which has a different cluster label, 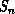 , then both
, then both
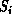 and
and 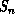 are set to the minimum of the two. This is continued until
nothing changes, by which time all the clusters will have been labelled with
the minimum initial label of all the sites in the cluster. Note that
checking termination of the algorithm involves each processor sending a
termination flag (finished or not finished) to every other processor after
each step, which can become very costly for a large processor array. This is
an SIMD algorithm and can, therefore, be run on machines like the AMT DAP and
TMC Connection Machine. However, the SIMD
nature of these computers leads to very poor load balancing. Most
processors end up waiting for the few in the largest cluster which are
the last to finish. We implemented this on the AMT DAP and obtained
only about 20% efficiency.
are set to the minimum of the two. This is continued until
nothing changes, by which time all the clusters will have been labelled with
the minimum initial label of all the sites in the cluster. Note that
checking termination of the algorithm involves each processor sending a
termination flag (finished or not finished) to every other processor after
each step, which can become very costly for a large processor array. This is
an SIMD algorithm and can, therefore, be run on machines like the AMT DAP and
TMC Connection Machine. However, the SIMD
nature of these computers leads to very poor load balancing. Most
processors end up waiting for the few in the largest cluster which are
the last to finish. We implemented this on the AMT DAP and obtained
only about 20% efficiency.
We can improve this method on a MIMD machine by using a faster
sequential algorithm, such as ``ants in the labyrinth,'' to label the
clusters in the sublattice on each processor, and then just use
self-labelling on the sites at the edges of each processor to
eventually arrive at the global cluster labels [Baillie:91a],
[Coddington:90a], [Flanigan:92a]. The number of steps
required to do the self-labelling will depend on the largest cluster
which, at the phase transition, will generally span the entire
lattice. The number of self-labelling steps will therefore be of the
order of the maximum distance between processors, which for a square
array of P processors is just 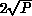 . Hence, the amount of
communication (and calculation) involved in doing the self-labelling,
which is proportional to the number of iterations times the perimeter
of the sublattice, behaves as L for an
. Hence, the amount of
communication (and calculation) involved in doing the self-labelling,
which is proportional to the number of iterations times the perimeter
of the sublattice, behaves as L for an 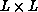 lattice; whereas, the time taken on each processor to do the local
cluster labelling is proportional to the area of the sublattice, which
is
lattice; whereas, the time taken on each processor to do the local
cluster labelling is proportional to the area of the sublattice, which
is 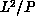 . Therefore, as long as L is substantially greater than
the number of processors, we can expect to obtain a reasonable
speedup. Of course, this algorithm suffers from the same type of load
imbalance as the SIMD version. However, in this case, it is much less
severe since most of the work is done with ``ants in the labyrinth,''
which is well load balanced. The speedups obtained
on the Symult 2010, for a variety of lattice sizes, are shown in
Figure 12.27. The dashed line indicates perfect speedup
(i.e., 100% efficiency). The lattice sizes for which we actually need
large numbers of processors are of the order of
. Therefore, as long as L is substantially greater than
the number of processors, we can expect to obtain a reasonable
speedup. Of course, this algorithm suffers from the same type of load
imbalance as the SIMD version. However, in this case, it is much less
severe since most of the work is done with ``ants in the labyrinth,''
which is well load balanced. The speedups obtained
on the Symult 2010, for a variety of lattice sizes, are shown in
Figure 12.27. The dashed line indicates perfect speedup
(i.e., 100% efficiency). The lattice sizes for which we actually need
large numbers of processors are of the order of 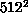 or greater, and
we can see that running on 64 nodes (or running multiple simulations of
64 nodes each) gives us quite acceptable efficiencies of about 70% for
or greater, and
we can see that running on 64 nodes (or running multiple simulations of
64 nodes each) gives us quite acceptable efficiencies of about 70% for
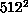 and 80% for
and 80% for 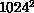 .
.
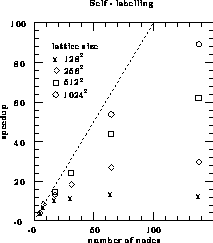
Figure 12.27: Speedups for Self-Labelling Algorithm





Next: 12.6.5 Global Equivalencing
Up: 12.6 Cluster Algorithms for
Previous: 12.6.3 Parallel Cluster Algorithms
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
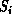 . In
practice, this is simply chosen as the position of that site in the lattice.
At each step of the algorithm in parallel, every site looks in turn at each
of its neighbors in the positive directions. If it is bonded to a
neighboring site, n, which has a different cluster label,
. In
practice, this is simply chosen as the position of that site in the lattice.
At each step of the algorithm in parallel, every site looks in turn at each
of its neighbors in the positive directions. If it is bonded to a
neighboring site, n, which has a different cluster label, 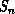 , then both
, then both
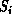 and
and 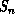 are set to the minimum of the two. This is continued until
nothing changes, by which time all the clusters will have been labelled with
the minimum initial label of all the sites in the cluster. Note that
checking termination of the algorithm involves each processor sending a
termination flag (finished or not finished) to every other processor after
each step, which can become very costly for a large processor array. This is
an SIMD algorithm and can, therefore, be run on machines like the AMT DAP and
TMC Connection Machine. However, the SIMD
nature of these computers leads to very poor load balancing. Most
processors end up waiting for the few in the largest cluster which are
the last to finish. We implemented this on the AMT DAP and obtained
only about 20% efficiency.
are set to the minimum of the two. This is continued until
nothing changes, by which time all the clusters will have been labelled with
the minimum initial label of all the sites in the cluster. Note that
checking termination of the algorithm involves each processor sending a
termination flag (finished or not finished) to every other processor after
each step, which can become very costly for a large processor array. This is
an SIMD algorithm and can, therefore, be run on machines like the AMT DAP and
TMC Connection Machine. However, the SIMD
nature of these computers leads to very poor load balancing. Most
processors end up waiting for the few in the largest cluster which are
the last to finish. We implemented this on the AMT DAP and obtained
only about 20% efficiency.





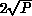 . Hence, the amount of
communication (and calculation) involved in doing the self-labelling,
which is proportional to the number of iterations times the perimeter
of the sublattice, behaves as L for an
. Hence, the amount of
communication (and calculation) involved in doing the self-labelling,
which is proportional to the number of iterations times the perimeter
of the sublattice, behaves as L for an 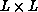 lattice; whereas, the time taken on each processor to do the local
cluster labelling is proportional to the area of the sublattice, which
is
lattice; whereas, the time taken on each processor to do the local
cluster labelling is proportional to the area of the sublattice, which
is 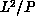 . Therefore, as long as L is substantially greater than
the number of processors, we can expect to obtain a reasonable
speedup. Of course, this algorithm suffers from the same type of load
imbalance as the SIMD version. However, in this case, it is much less
severe since most of the work is done with ``ants in the labyrinth,''
which is well load balanced.
. Therefore, as long as L is substantially greater than
the number of processors, we can expect to obtain a reasonable
speedup. Of course, this algorithm suffers from the same type of load
imbalance as the SIMD version. However, in this case, it is much less
severe since most of the work is done with ``ants in the labyrinth,''
which is well load balanced.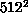 or greater, and
we can see that running on 64 nodes (or running multiple simulations of
64 nodes each) gives us quite acceptable efficiencies of about 70% for
or greater, and
we can see that running on 64 nodes (or running multiple simulations of
64 nodes each) gives us quite acceptable efficiencies of about 70% for
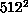 and 80% for
and 80% for 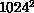 .
.
