




Next: 11.4.4 Results
Up: An Improved Method
Previous: Background on Markov
Simulated annealing does not take
advantage of the local opt heuristics. This means that instead of
sampling local opt tours as does L-K repeated from random starts,
the chain samples all tours. It would be a great advantage to be able
to restrict the sampling of a Markov chain to the local opt tours
only. Then the bias which the Markov chain provides would enable one
to sample the shortest local opt tours more efficiently than local opt
repeated from random starts. This is what our new algorithm does.
To do this, one has to find a way to go from one local opt tour, 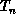 , to
another,
, to
another, 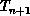 , and this is the heart of our procedure. We propose to do
a change on
, and this is the heart of our procedure. We propose to do
a change on 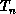 , which we call a ``kick.'' This can be a random p-change,
for instance, but we will choose something smarter than that. Follow this
kick by the local opt tour improvement heuristic until reaching a new local
opt tour
, which we call a ``kick.'' This can be a random p-change,
for instance, but we will choose something smarter than that. Follow this
kick by the local opt tour improvement heuristic until reaching a new local
opt tour 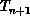 . Then accept or reject
. Then accept or reject 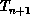 depending on the
increase or decrease in tour length compared to
depending on the
increase or decrease in tour length compared to 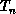 . This is illustrated
in Figure 11.24. Since there are many changes in going from
. This is illustrated
in Figure 11.24. Since there are many changes in going from 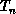 to
to 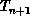 , we call this method a ``Large-Step Markov Chain.'' It can
also be called ``Iterated Local Opt,'' but it should be realized that it is
precisely finding a way to iterate which is the difficulty! The algorithm is
far better than the small-step Markov chain methods (conventional simulated
annealing) because the accept/reject procedure is not implemented on the
intermediate tours which are almost always of longer length. Instead, the
accept/reject does not happen until the system has returned to a local
minimum. The method directly steps from one local minimum to another. It is
thus much easier to escape from local minima.
, we call this method a ``Large-Step Markov Chain.'' It can
also be called ``Iterated Local Opt,'' but it should be realized that it is
precisely finding a way to iterate which is the difficulty! The algorithm is
far better than the small-step Markov chain methods (conventional simulated
annealing) because the accept/reject procedure is not implemented on the
intermediate tours which are almost always of longer length. Instead, the
accept/reject does not happen until the system has returned to a local
minimum. The method directly steps from one local minimum to another. It is
thus much easier to escape from local minima.
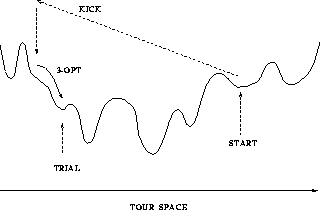
Figure 11.24: Schematic Representation of the Objective Function and of the
Tour Modification Procedure Used in the Large-step Markov Chain
At this point, let us mention that this method is no longer a true
simulated annealing algorithm. That is, the algorithm does NOT
correspond to the simulation of any physical system undergoing
annealing. The reason is that a certain symmetry property, termed
``detailed balance'' in the physics community,
is not satisfied by the large-step algorithm. [Martin:91a] says a
bit more about this. One consequence of this is that the parameter
``temperature'' which one anneals with no longer plays the role of a
true, physical temperature-instead it is merely a parameter which
controls the bias towards the optimum. The lack of a physical analogy
may be the reason that this algorithm has not been tried before, even
though much more exotic algorithms (such as appealing to quantum
mechanical analogies!) have been proposed.
We have found that in practice, this methodology provides an efficient
sampling of the local opt tours. There are a number of criteria which need
to be met for the biased sampling of the Markov chain to be more efficient
than plain random sampling. These conditions are satisfied for the TSP, and
more generally whenever local search heuristics are useful. Let us stress
before proceeding to specifics that this large-step Markov chain approach is
extremely general, being applicable to any optimization
problem where one has local search heuristics. It enables one to get a
performance which is at least as good as local search, with substantial
improvements over that if the sampling can be biased effectively.
Finally, although the method is general, it can be adapted to match the
problem of interest through the choice of the kick. We will now
discuss how to choose the kick for the TSP.
Consider, for instance, the case where the local search is three-opt. If we
used a kick consisting of a three-change, the three-opt would very often
simply bring us back to the previous tour with no gain. Thus, it is probably
a good idea to go to a four-change for the kick when the local search is
three-opt. For more general local search algorithms, a good choice for the
kick would be a k-change which does not occur in the local search.
Surprisingly, it turns out that two-opt, three-opt, and especially L-K
are structured so that there is one kick choice which is natural for all of
them. To see this, it is useful to go back to the paper by Lin and
Kernighan. In that paper, they define ``sequential'' changes and they also show
that if the tour is to be improved, one can force all the partial gains during
the k-change to be positive. A consequence of this is that the
checkout time for sequential k-changes can be completed in 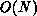 steps.
It is easy to see that all two and three changes are sequential, and that the
first nonsequential change occurs at k=4 (Figure 2 of their paper). We
call this graph a ``double-bridge'' change because of what it does to the tour.
It can be constructed by first doing a two-change which disconnects the tour;
the second two-change must then reconnect the two parts, thereby creating a
bridge. Note that both of the two-changes are bridges in their own way, and
that the double-bridge change is the only nonsequential four-change which
cannot be obtained by composing changes which are both sequential and leave
the tour connected. If we included this double-bridge change in the
definition of the neighborhood for a local search, checkout time would
require
steps.
It is easy to see that all two and three changes are sequential, and that the
first nonsequential change occurs at k=4 (Figure 2 of their paper). We
call this graph a ``double-bridge'' change because of what it does to the tour.
It can be constructed by first doing a two-change which disconnects the tour;
the second two-change must then reconnect the two parts, thereby creating a
bridge. Note that both of the two-changes are bridges in their own way, and
that the double-bridge change is the only nonsequential four-change which
cannot be obtained by composing changes which are both sequential and leave
the tour connected. If we included this double-bridge change in the
definition of the neighborhood for a local search, checkout time would
require 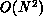 steps (a factor N for each bridge essentially). Rather
than doing this change as part of the local search, we include such changes
stochastically as our kick. The double-bridge kick is the most natural
choice for any local search method which considers only sequential changes.
Because L-K does so many changes for k greater than three, but misses
double-bridges, one can expect that most of what remains in excess length
using L-K might be removed with our extension. The results below
indicate that this is the case.
steps (a factor N for each bridge essentially). Rather
than doing this change as part of the local search, we include such changes
stochastically as our kick. The double-bridge kick is the most natural
choice for any local search method which considers only sequential changes.
Because L-K does so many changes for k greater than three, but misses
double-bridges, one can expect that most of what remains in excess length
using L-K might be removed with our extension. The results below
indicate that this is the case.





Next: 11.4.4 Results
Up: An Improved Method
Previous: Background on Markov
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
 , to
another,
, to
another, 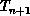 , and this is the heart of our procedure. We propose to do
a change on
, and this is the heart of our procedure. We propose to do
a change on 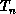 , which we call a ``kick.'' This can be a random p-change,
for instance, but we will choose something smarter than that. Follow this
kick by the local opt tour improvement heuristic until reaching a new local
opt tour
, which we call a ``kick.'' This can be a random p-change,
for instance, but we will choose something smarter than that. Follow this
kick by the local opt tour improvement heuristic until reaching a new local
opt tour 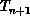 . Then accept or reject
. Then accept or reject 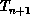 depending on the
increase or decrease in tour length compared to
depending on the
increase or decrease in tour length compared to 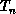 . This is illustrated
in Figure 11.24. Since there are many changes in going from
. This is illustrated
in Figure 11.24. Since there are many changes in going from 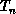 to
to 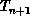 , we call this method a ``Large-Step Markov Chain.'' It can
also be called ``Iterated Local Opt,'' but it should be realized that it is
precisely finding a way to iterate which is the difficulty! The algorithm is
far better than the small-step Markov chain methods (conventional simulated
annealing) because the accept/reject procedure is not implemented on the
intermediate tours which are almost always of longer length. Instead, the
accept/reject does not happen until the system has returned to a local
minimum. The method directly steps from one local minimum to another. It is
thus much easier to escape from local minima.
, we call this method a ``Large-Step Markov Chain.'' It can
also be called ``Iterated Local Opt,'' but it should be realized that it is
precisely finding a way to iterate which is the difficulty! The algorithm is
far better than the small-step Markov chain methods (conventional simulated
annealing) because the accept/reject procedure is not implemented on the
intermediate tours which are almost always of longer length. Instead, the
accept/reject does not happen until the system has returned to a local
minimum. The method directly steps from one local minimum to another. It is
thus much easier to escape from local minima.






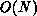 steps.
It is easy to see that all two and three changes are sequential, and that the
first nonsequential change occurs at k=4 (Figure 2 of their paper). We
call this graph a ``double-bridge'' change because of what it does to the tour.
It can be constructed by first doing a two-change which disconnects the tour;
the second two-change must then reconnect the two parts, thereby creating a
bridge. Note that both of the two-changes are bridges in their own way, and
that the double-bridge change is the only nonsequential four-change which
cannot be obtained by composing changes which are both sequential and leave
the tour connected. If we included this double-bridge change in the
definition of the neighborhood for a local search, checkout time would
require
steps.
It is easy to see that all two and three changes are sequential, and that the
first nonsequential change occurs at k=4 (Figure 2 of their paper). We
call this graph a ``double-bridge'' change because of what it does to the tour.
It can be constructed by first doing a two-change which disconnects the tour;
the second two-change must then reconnect the two parts, thereby creating a
bridge. Note that both of the two-changes are bridges in their own way, and
that the double-bridge change is the only nonsequential four-change which
cannot be obtained by composing changes which are both sequential and leave
the tour connected. If we included this double-bridge change in the
definition of the neighborhood for a local search, checkout time would
require 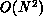 steps (a factor N for each bridge essentially). Rather
than doing this change as part of the local search, we include such changes
stochastically as our kick. The double-bridge kick is the most natural
choice for any local search method which considers only sequential changes.
Because L-K does so many changes for k greater than three, but misses
double-bridges, one can expect that most of what remains in excess length
using L-K might be removed with our extension. The results below
indicate that this is the case.
steps (a factor N for each bridge essentially). Rather
than doing this change as part of the local search, we include such changes
stochastically as our kick. The double-bridge kick is the most natural
choice for any local search method which considers only sequential changes.
Because L-K does so many changes for k greater than three, but misses
double-bridges, one can expect that most of what remains in excess length
using L-K might be removed with our extension. The results below
indicate that this is the case.