




Next: 11.4.1 Background on Local
Up: 11 Load Balancing and
Previous: 11.3 Physical Optimization
The Travelling Salesman Problem (TSP) is probably the most well-known
member of the wider field of combinatorial
optimization (CO) problems. These are difficult
optimization problems where the set of feasible solutions (trial
solutions which satisfy the constraints of the problem but are not
necessarily optimal) is a finite, though usually very large set. The
number of feasible solutions grows as some combinatoric factor such as
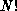 , where N characterizes the size of the problem. We have already
commented on the use of neural networks for the TSP in the previous
section. Here we show how to combine problem-specific heuristics with
simulated annealing, a physical optimization method.
, where N characterizes the size of the problem. We have already
commented on the use of neural networks for the TSP in the previous
section. Here we show how to combine problem-specific heuristics with
simulated annealing, a physical optimization method.
It has often been the case that progress on the TSP has led to progress
on many CO problems and more general optimization problems. In this
way, the TSP is a playground for the study of CO problems. Though the
present work concentrates on the TSP, a number of our ideas are general
and apply to all optimization problems.
The most significant issues occur as one tries to find extremely good
or exact solutions to the TSP. Many algorithms exist which are fast
and find feasible solutions which are within a few percent of the
optimum length. Here, we present algorithms which will usually find
exact solutions to substantial instances of the TSP. We are limited by
space considerations to a brief presentation of the method-more
details may be found in [Martin:91a].
In a general instance of the TSP one is given N ``cities'' and a
matrix 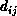 giving the distance or cost function for going from
city i to j. Without loss of generality, the distances can be
assumed to be positive. A ``tour'' consists of a list of N cities,
giving the distance or cost function for going from
city i to j. Without loss of generality, the distances can be
assumed to be positive. A ``tour'' consists of a list of N cities,
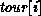 , where each city appears once and only once. In the TSP, the
problem is to find the tour with the minimum ``length,'' where length
is defined to be the sum of the lengths along each step of the tour,
, where each city appears once and only once. In the TSP, the
problem is to find the tour with the minimum ``length,'' where length
is defined to be the sum of the lengths along each step of the tour,
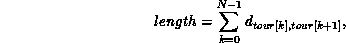
and 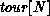 is
identified with
is
identified with 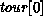 to make it periodic.
to make it periodic.
Most common instances of the TSP have a symmetric distance matrix; we
will hereafter focus on this case. All CO problems can be formulated
as optimizing an objective function (e.g., the length) subject to
constraints (e.g., legal tours).





Next: 11.4.1 Background on Local
Up: 11 Load Balancing and
Previous: 11.3 Physical Optimization
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
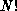 , where N characterizes the size of the problem. We have already
commented on the use of neural networks for the TSP in the previous
section. Here we show how to combine problem-specific heuristics with
simulated annealing, a physical optimization method.
, where N characterizes the size of the problem. We have already
commented on the use of neural networks for the TSP in the previous
section. Here we show how to combine problem-specific heuristics with
simulated annealing, a physical optimization method.





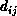 giving the distance or cost function for going from
city i to j. Without loss of generality, the distances can be
assumed to be positive. A ``tour'' consists of a list of N cities,
giving the distance or cost function for going from
city i to j. Without loss of generality, the distances can be
assumed to be positive. A ``tour'' consists of a list of N cities,
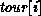 , where each city appears once and only once. In the TSP, the
problem is to find the tour with the minimum ``length,'' where length
is defined to be the sum of the lengths along each step of the tour,
, where each city appears once and only once. In the TSP, the
problem is to find the tour with the minimum ``length,'' where length
is defined to be the sum of the lengths along each step of the tour, 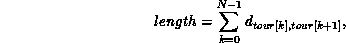
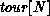 is
identified with
is
identified with 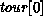 to make it periodic.
to make it periodic.