




Next: 9.5.7 Conclusions
Up: 9.5.6 Performance
Previous: Order 13040 Example
Now, we turn to a timing example of an order 2500 sparse, random matrix. The
matrix has a random diagonal, plus 2 percent random fill of the
off-diagonals; entries have a dynamic range of 0-10,000. Normally, data is
averaged over random matrices for each grid shape (as noted), and over four
repetitive runs for each random matrix. Partial row pivoting was used
exclusively. Table 9.5 compiles timings for various grid shapes
of row-scatter/column-scatter, and row-scatter/column-(S=10)
distributions, for as few as nine nodes and as many as 128. Memory
limitations set the lower bound on the number of nodes.
This example demonstrates that speedups are possible for this reasonably
small sparse example with this general-purpose solver, and that the
one-parameter distribution is critical to achieving overall better performance
even for this random, essentially unstructured example. Without the
one-parameter distribution, triangular-solve performance is poor, except in
grid configurations where the factorization is itself degraded (e.g.,
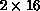 ). Furthermore, the choice of S=10 is universally reasonable
for the Q > 1 grid shapes illustrated here, so the distribution proves easy
to tune for this type of matrix. We are able to maintain an almost constant
speed for the triangular solves while increasing speed for both the A-mode
and B-mode factorizations. We presume, based on experience, that
triangular-solve times are comparable to the sequential solution
times-further study is needed in this area to see if and how
performance can be improved. The consistent A-mode to B-mode ratio of
approximately two is attributed primarily to reduced communication
costs in B-mode, realized through the elimination of essentially all
combine operations in B-mode.
). Furthermore, the choice of S=10 is universally reasonable
for the Q > 1 grid shapes illustrated here, so the distribution proves easy
to tune for this type of matrix. We are able to maintain an almost constant
speed for the triangular solves while increasing speed for both the A-mode
and B-mode factorizations. We presume, based on experience, that
triangular-solve times are comparable to the sequential solution
times-further study is needed in this area to see if and how
performance can be improved. The consistent A-mode to B-mode ratio of
approximately two is attributed primarily to reduced communication
costs in B-mode, realized through the elimination of essentially all
combine operations in B-mode.
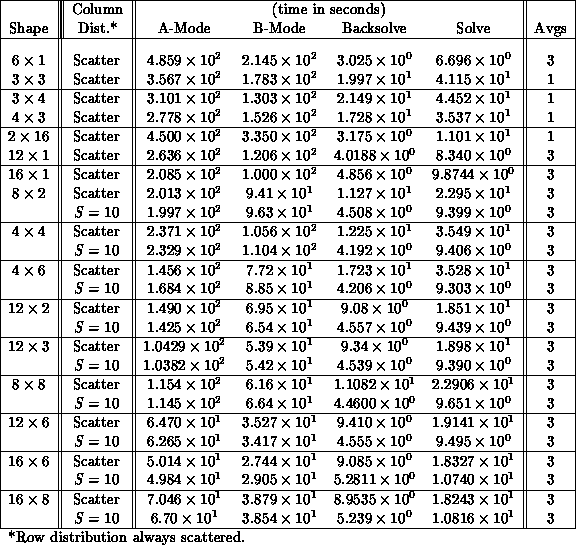
Table 9.5: Order 2500 Matrix Performance. Performance is a function of grid
shape and size, and S-parameter. ``Best'' performance is for the
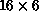 grid with S=10.
grid with S=10.
While triangular-solve performance exemplifies sequentialism in the
algorithm, it should be noted that we do achieve significant overall
performance improvements between 6 nodes and 96 (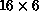 grid) nodes,
and that the repeatedly used B-mode factorization remains dominant compared
to the triangular solves even for 128 nodes. Consequently, efforts aimed
at increasing performance of the B-mode factorization (at the expense
of additional A-mode work) are interesting to consider. For the
factorizations, we also expect that we are achieving nontrivial speedups
relative to one node, but we are unable to quantify this at present because
of the memory limitations alluded to above.
grid) nodes,
and that the repeatedly used B-mode factorization remains dominant compared
to the triangular solves even for 128 nodes. Consequently, efforts aimed
at increasing performance of the B-mode factorization (at the expense
of additional A-mode work) are interesting to consider. For the
factorizations, we also expect that we are achieving nontrivial speedups
relative to one node, but we are unable to quantify this at present because
of the memory limitations alluded to above.





Next: 9.5.7 Conclusions
Up: 9.5.6 Performance
Previous: Order 13040 Example
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
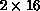 ). Furthermore, the choice of S=10 is universally reasonable
for the Q > 1 grid shapes illustrated here, so the distribution proves easy
to tune for this type of matrix. We are able to maintain an almost constant
speed for the triangular solves while increasing speed for both the A-mode
and B-mode factorizations. We presume, based on experience, that
triangular-solve times are comparable to the sequential solution
times-further study is needed in this area to see if and how
performance can be improved. The consistent A-mode to B-mode ratio of
approximately two is attributed primarily to reduced communication
costs in B-mode, realized through the elimination of essentially all
combine operations in B-mode.
). Furthermore, the choice of S=10 is universally reasonable
for the Q > 1 grid shapes illustrated here, so the distribution proves easy
to tune for this type of matrix. We are able to maintain an almost constant
speed for the triangular solves while increasing speed for both the A-mode
and B-mode factorizations. We presume, based on experience, that
triangular-solve times are comparable to the sequential solution
times-further study is needed in this area to see if and how
performance can be improved. The consistent A-mode to B-mode ratio of
approximately two is attributed primarily to reduced communication
costs in B-mode, realized through the elimination of essentially all
combine operations in B-mode.






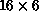 grid with S=10.
grid with S=10.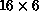 grid) nodes,
and that the repeatedly used B-mode factorization remains dominant compared
to the triangular solves even for 128 nodes. Consequently, efforts aimed
at increasing performance of the B-mode factorization (at the expense
of additional A-mode work) are interesting to consider. For the
factorizations, we also expect that we are achieving nontrivial speedups
relative to one node, but we are unable to quantify this at present because
of the memory limitations alluded to above.
grid) nodes,
and that the repeatedly used B-mode factorization remains dominant compared
to the triangular solves even for 128 nodes. Consequently, efforts aimed
at increasing performance of the B-mode factorization (at the expense
of additional A-mode work) are interesting to consider. For the
factorizations, we also expect that we are achieving nontrivial speedups
relative to one node, but we are unable to quantify this at present because
of the memory limitations alluded to above.