




Next: Concurrent DASSL Applied
Up: LU Factorization of
Previous: Order 2500 Example
There are several classes of future work to be considered. First, we
need to take the A-mode ``analyze'' phase to its logical completion, by
including pivot-order sorting of the 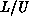 pointer structures to
improve performance for systems that should demonstrate subquadratic
sequential complexity. This will require minor modifications to B-mode
(that already takes advantage of column-traversing elimination), to
reduce testing for inactive rows as the elimination progresses. We
already realize optimal computation work in the triangular solves, and
we mitigate the effect of Q > 1 quadratic communication work using
the one-parameter distribution.
pointer structures to
improve performance for systems that should demonstrate subquadratic
sequential complexity. This will require minor modifications to B-mode
(that already takes advantage of column-traversing elimination), to
reduce testing for inactive rows as the elimination progresses. We
already realize optimal computation work in the triangular solves, and
we mitigate the effect of Q > 1 quadratic communication work using
the one-parameter distribution.
Second, we need to exploit ``timelike'' concurrency in linear
algebra-multiple pivots. This has been addressed by Alaghband for
shared-memory implementations of MA28 with 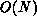 -complexity
heuristics [Alaghband:89a]. These efforts must be reconsidered in the
multicomputer setting and effective variations must be devised. This
approach should prove an important source of additional speedup for many
chemical engineering applications, because
of the tendency towards extreme sparsity, with mainly band and/or
block-diagonal structure.
-complexity
heuristics [Alaghband:89a]. These efforts must be reconsidered in the
multicomputer setting and effective variations must be devised. This
approach should prove an important source of additional speedup for many
chemical engineering applications, because
of the tendency towards extreme sparsity, with mainly band and/or
block-diagonal structure.
Third, we could exploit new communication strategies and data
redistribution. Within a process grid, we could incrementally
redistribute 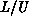 by utilizing the inherent broadcasts of L columns
and U rows to improve load balance in the
triangular solves at the expense of slightly more factorization
computational overhead and significantly more memory overhead (a factor
of nearly two). Memory overhead could be reduced at the expense of
further communication if explicit pivoting were used concomitantly.
by utilizing the inherent broadcasts of L columns
and U rows to improve load balance in the
triangular solves at the expense of slightly more factorization
computational overhead and significantly more memory overhead (a factor
of nearly two). Memory overhead could be reduced at the expense of
further communication if explicit pivoting were used concomitantly.
Fourth, we can develop adaptive broadcast algorithms
that track the known load imbalance in the B-mode factorization, and
shift greater communication emphasis to nodes with less computational
work remaining. For example, the pivot column is naturally a ``hot
spot" because the multiplier column (L column) must be computed
before broadcast to the awaiting process columns.
Allowing the non-pivot columns to handle the majority of the
communication could be beneficial, even though this implies additional
overall communication. Similarly, we might likewise apply this to the
pivot row broadcast , and especially for the pivot
process, because it must participate in two broadcast
operations.
We could utilize two process grids. When rows (columns) of 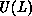 are
broadcast , extra broadcasts to a
secondary process grid could reasonably be included. The secondary
process grid could work on redistributing
are
broadcast , extra broadcasts to a
secondary process grid could reasonably be included. The secondary
process grid could work on redistributing 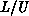 to an efficient process
grid shape and size for triangular solves while the factorization
continues on the primary grid. This overlapping of communication and
computation could also be used to reduce the cost of transposing the
solution vector from column-distributed to row-distributed, which
normally follows the triangular solves.
to an efficient process
grid shape and size for triangular solves while the factorization
continues on the primary grid. This overlapping of communication and
computation could also be used to reduce the cost of transposing the
solution vector from column-distributed to row-distributed, which
normally follows the triangular solves.
The sparse solver supports arbitrary user-defined pivoting strategies. We
have considered but not fully explored issues of fill-reduction versus
minimum time; in particular we have implemented a Markowitz-count
fill-reduction strategy [Duff:86a]. Study of the usefulness of partial
column pivoting and other strategies is also needed. We will report on this
in the future.
Reduced-communication pivoting and parametric distributions can be applied
immediately to concurrent dense solvers with definite improvements in
performance. While triangular solves remain lower-order work in the dense
case, and may sensibly admit less tuning in S, the reduction of pivot
communication is certain to improve performance. A new dense solver
exploiting these ideas is under construction at present.
In closing, we suggest that the algorithms generating the sequences of
sparse matrices must themselves be reconsidered in the concurrent setting.
Changes that introduce multiple right-hand sides could help to amortize
linear algebra cost over multiple timelike steps of the higher level
algorithm. Because of inevitable load imbalance, idle processor time is
essentially free-algorithms that find ways to use this time by asking for
more speculative (partial) solutions appear useful in working towards
higher performance.
This work was performed by Anthony Skjellum and Alvin Leung while the
latter held a Caltech Summer Undergraduate Research Fellowship. A
helpful contribution was the dense concurrent linear algebra library
provided by Eric Van de Velde, as well as his prototype sparse
concurrent linear algebra library.





Next: Concurrent DASSL Applied
Up: LU Factorization of
Previous: Order 2500 Example
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
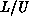 pointer structures to
improve performance for systems that should demonstrate subquadratic
sequential complexity. This will require minor modifications to B-mode
(that already takes advantage of column-traversing elimination), to
reduce testing for inactive rows as the elimination progresses. We
already realize optimal computation work in the triangular solves, and
we mitigate the effect of Q > 1 quadratic communication work using
the one-parameter distribution.
pointer structures to
improve performance for systems that should demonstrate subquadratic
sequential complexity. This will require minor modifications to B-mode
(that already takes advantage of column-traversing elimination), to
reduce testing for inactive rows as the elimination progresses. We
already realize optimal computation work in the triangular solves, and
we mitigate the effect of Q > 1 quadratic communication work using
the one-parameter distribution.





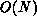 -complexity
heuristics [
-complexity
heuristics [ by utilizing the inherent broadcasts of L columns
and U rows to improve load balance
by utilizing the inherent broadcasts of L columns
and U rows to improve load balance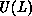 are
broadcast
are
broadcast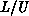 to an efficient process
grid shape and size for triangular solves while the factorization
continues on the primary grid. This overlapping of communication and
computation could also be used to reduce the cost of transposing the
solution vector from column-distributed to row-distributed, which
normally follows the triangular solves.
to an efficient process
grid shape and size for triangular solves while the factorization
continues on the primary grid. This overlapping of communication and
computation could also be used to reduce the cost of transposing the
solution vector from column-distributed to row-distributed, which
normally follows the triangular solves.