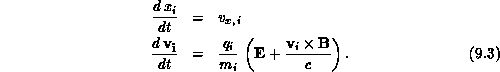
The parallel one-dimensional electrostatic code was modified to include the effects of external and self-consistent magnetic fields. This one-dimensional electromagnetic code, with kinetic electrons and ions, has been used to study electron dynamics in oblique collisionless shock waves such as in the earth's bow shock. Forces on the particles are found from the fields at the grid points by interpolation. For this code, with variation in the x direction only, the orbit equations for the iparticle are
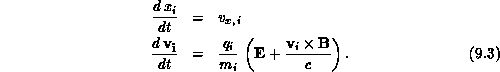
Motion is followed in the x direction only, but all three velocity
components must be calculated in order to calculate the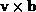 
force. The longitudinal (along x) electric field is found by solving
Poisson's equation
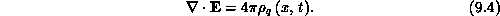
The transverse (to x) electromagnetic fields,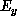 
, 
, 
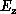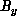, and
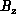, are found by solving
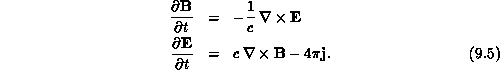
Table 9.2: Comparison of Push Times on Various Computers
The plasma current density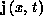 
and charge density
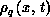are found at the grid points by interpolation from the
particle positions. Only the transverse (y and z) components of the
plasma current are needed. These coupled particle and field equations are
solved in time as an initial value problem. As in the electrostatic code,
the fields are solved by Fourier-transforming the charge and
current densities and solving the equation in k space, and advancing
the Fourier components in time. External fields and currents can also
be included. At each time step, the fields are transformed back to
configuration space to calculate the forces needed to advance the
particles to the next time step. The hypercube FFT routine
described in Section 12.4 was used in the one-dimensional
codes. Extending the existing parallel electrostatic code to include
the electromagnetic effects required no change in the parallel
decomposition of the code.