




Next: 8.2.3 Parallel Algorithm
Up: Quantum Mechanical Reactive
Previous: 8.2.1 Introduction
The detailed formulation of reactive scattering based on hyperspherical
coordinates and local variational hyperspherical surface functions (LHSF) is
discussed elsewhere [Kuppermann:86a], [Hipes:87a],
[Cuccaro:89a]. We present a very brief review to facilitate the
explanation of the parallel algorithms.
For a triatomic system, we label the three atoms 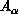 ,
,
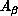 and
and 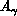 . Let (
. Let (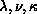 ) be any cyclic
permutation of the indices (
) be any cyclic
permutation of the indices (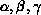 ). We define the
). We define the
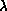 coordinates, the mass-scaled [Delves:59a;62a]
internuclear vector
coordinates, the mass-scaled [Delves:59a;62a]
internuclear vector 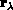 from
from 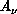 to
to 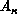 , and the mass-scaled
position vector
, and the mass-scaled
position vector 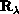 of
of 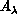 with respect to
the center of mass of
with respect to
the center of mass of 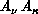 diatom. The symmetrized
hyperspherical coordinates [Kuppermann:75a] are the hyper-radius
diatom. The symmetrized
hyperspherical coordinates [Kuppermann:75a] are the hyper-radius
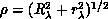 , and a set of five angles
, and a set of five angles
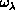 ,
, 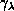 ,
, 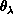 ,
,
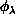 and
and 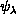 , denoted collectively as
, denoted collectively as
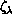 . The first two of these are in the range 0 to
. The first two of these are in the range 0 to
 and are, respectively,
and are, respectively, 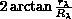 and
the angle between
and
the angle between 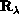 and
and 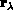 . The
angles
. The
angles 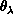 ,
, 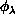 are the polar angles of
are the polar angles of 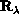 in a space-fixed frame and
in a space-fixed frame and 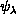 is the tumbling
angle of the
is the tumbling
angle of the 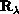 ,
, 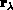 half-plane around
its edge
half-plane around
its edge 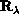 . The Hamiltonian
. The Hamiltonian 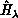 is
the sum of a radial kinetic energy operator term in
is
the sum of a radial kinetic energy operator term in 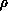 , and the
surface Hamiltonian
, and the
surface Hamiltonian 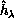 , which contains all differential
operators in
, which contains all differential
operators in 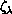 and the electronically adiabatic potential
and the electronically adiabatic potential
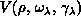 . The surface
Hamiltonian
. The surface
Hamiltonian 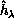 depends on
depends on 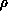 parametrically and is
therefore the ``frozen'' hyperradius part of
parametrically and is
therefore the ``frozen'' hyperradius part of 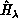 .
.
The scattering wave function 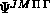 is labelled by
the total angular momentum J, its projection M on the
laboratory-fixed Z axis, the inversion parity
is labelled by
the total angular momentum J, its projection M on the
laboratory-fixed Z axis, the inversion parity 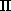 with respect to
the center of mass of the system, and the irreducible representation
with respect to
the center of mass of the system, and the irreducible representation
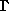 of the permutation group of the system (
of the permutation group of the system (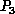 for
for 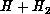 ) to
which the electronuclear wave function, excluding the nuclear spin part,
belongs [Lepetit:90a;90b]. It can be expanded in terms of the
LHSF
) to
which the electronuclear wave function, excluding the nuclear spin part,
belongs [Lepetit:90a;90b]. It can be expanded in terms of the
LHSF 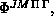 defined below, and calculated at the values
defined below, and calculated at the values
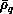 of
of 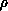 :
:
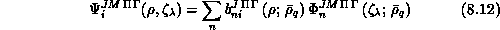
The index i is introduced to permit consideration of a set of many
linearly independent solutions of the Schrödinger equation corresponding to
distinct initial conditions which are needed to obtain the appropriate
scattering matrices.
The LHSF 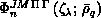 and
associated energies
and
associated energies 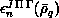 are,
respectively, the eigenfunctions and eigenvalues
of the surface Hamiltonian
are,
respectively, the eigenfunctions and eigenvalues
of the surface Hamiltonian 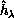 . They are obtained using
a variational approach [Cuccaro:89a]. The variational basis set
consists of products of Wigner rotation matrices
. They are obtained using
a variational approach [Cuccaro:89a]. The variational basis set
consists of products of Wigner rotation matrices
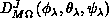 ,
associated Legendre functions of
,
associated Legendre functions of 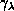 and functions of
and functions of
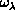 which depend parametically on
which depend parametically on 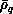 and are
obtained from the numerical solution of one-dimensional
eigenvalue-eigenfunction differential equations in
and are
obtained from the numerical solution of one-dimensional
eigenvalue-eigenfunction differential equations in 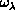 ,
involving a potential related to
,
involving a potential related to
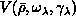 .
.
The variational method leads to an eigenvalue problem with coefficient and
overlap matrices 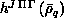 and
and
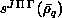 and whose elements are five-dimensional
integrals involving the variational basis functions.
and whose elements are five-dimensional
integrals involving the variational basis functions.
The coefficients 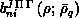 defined by
Equation 8.12 satisfy a coupled set of second-order
differential equations involving an interaction matrix
defined by
Equation 8.12 satisfy a coupled set of second-order
differential equations involving an interaction matrix
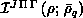 whose elements are defined
by
whose elements are defined
by
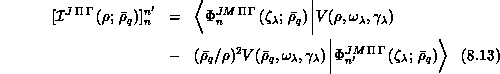
The configuration space 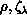 is divided into a set of Q
hyperspherical shells
is divided into a set of Q
hyperspherical shells 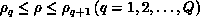 within each of which we choose a value
within each of which we choose a value 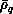 used in
expansion 8.12.
used in
expansion 8.12.
When changing from the LHSF set at 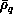 to the one at
to the one at
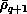 , neither
, neither 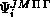 nor its derivative with
respect to
nor its derivative with
respect to 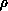 should change. This imposes continuity conditions on the
should change. This imposes continuity conditions on the
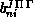 and their
and their 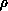 -derivatives at
-derivatives at 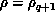 ,
involving the overlap matrix
,
involving the overlap matrix 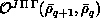 between the LHSF evaluated at
between the LHSF evaluated at 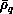 and
and
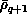
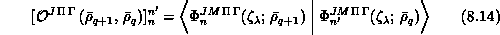
The five-dimensional integrals required to evaluate the elements of
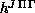 ,
, 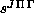 ,
, 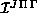 , and
, and
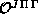 are performed analytically over
are performed analytically over 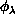 ,
,
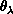 , and
, and 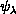 and by two-dimensional numerical
quadratures over
and by two-dimensional numerical
quadratures over 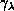 and
and 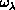 . These
quadratures account for 90% of the total time needed to calculate the LHSF
. These
quadratures account for 90% of the total time needed to calculate the LHSF
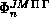 and the matrices
and the matrices 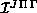 and
and
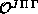 .
.
The system of second-order ordinary differential equations in the 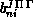 is integrated
as an initial value problem from small values of
is integrated
as an initial value problem from small values of 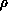 to large values
using Manolopoulos' logarithmic derivative propagator
[Manolopoulos:86a]. Matrix inversions account for more than 90%
of the time used by this propagator. All aspects of the physics can be
extracted from the solutions at large
to large values
using Manolopoulos' logarithmic derivative propagator
[Manolopoulos:86a]. Matrix inversions account for more than 90%
of the time used by this propagator. All aspects of the physics can be
extracted from the solutions at large 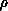 by a constant
by a constant 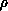 projection [Hipes:87a], [Hood:86a], [Kuppermann:86a].
projection [Hipes:87a], [Hood:86a], [Kuppermann:86a].





Next: 8.2.3 Parallel Algorithm
Up: Quantum Mechanical Reactive
Previous: 8.2.1 Introduction
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
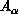 ,
,
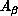 and
and 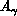 . Let (
. Let (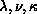 ) be any cyclic
permutation of the indices (
) be any cyclic
permutation of the indices (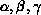 ). We define the
). We define the
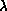 coordinates, the mass-scaled [Delves:59a;62a]
internuclear vector
coordinates, the mass-scaled [Delves:59a;62a]
internuclear vector 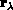 from
from 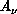 to
to 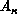 , and the mass-scaled
position vector
, and the mass-scaled
position vector 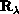 of
of 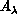 with respect to
the center of mass of
with respect to
the center of mass of 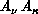 diatom. The symmetrized
hyperspherical coordinates [Kuppermann:75a] are the hyper-radius
diatom. The symmetrized
hyperspherical coordinates [Kuppermann:75a] are the hyper-radius
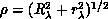 , and a set of five angles
, and a set of five angles
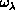 ,
, 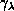 ,
, 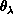 ,
,
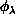 and
and 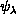 , denoted collectively as
, denoted collectively as
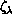 . The first two of these are in the range 0 to
. The first two of these are in the range 0 to
 and are, respectively,
and are, respectively, 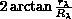 and
the angle between
and
the angle between 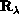 and
and 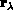 . The
angles
. The
angles 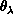 ,
, 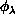 are the polar angles of
are the polar angles of 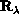 in a space-fixed frame and
in a space-fixed frame and 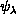 is the tumbling
angle of the
is the tumbling
angle of the 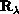 ,
, 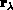 half-plane around
its edge
half-plane around
its edge 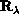 . The Hamiltonian
. The Hamiltonian 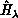 is
the sum of a radial kinetic energy operator term in
is
the sum of a radial kinetic energy operator term in 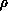 , and the
surface Hamiltonian
, and the
surface Hamiltonian 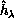 , which contains all differential
operators in
, which contains all differential
operators in 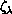 and the electronically adiabatic potential
and the electronically adiabatic potential
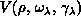 . The surface
Hamiltonian
. The surface
Hamiltonian 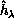 depends on
depends on 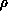 parametrically and is
therefore the ``frozen'' hyperradius part of
parametrically and is
therefore the ``frozen'' hyperradius part of 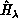 .
.





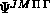 is labelled by
the total angular momentum J, its projection M on the
laboratory-fixed Z axis, the inversion parity
is labelled by
the total angular momentum J, its projection M on the
laboratory-fixed Z axis, the inversion parity 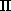 with respect to
the center of mass of the system, and the irreducible representation
with respect to
the center of mass of the system, and the irreducible representation
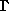 of the permutation group of the system (
of the permutation group of the system (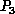 for
for 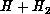 ) to
which the electronuclear wave function, excluding the nuclear spin part,
belongs [Lepetit:90a;90b]. It can be expanded in terms of the
LHSF
) to
which the electronuclear wave function, excluding the nuclear spin part,
belongs [Lepetit:90a;90b]. It can be expanded in terms of the
LHSF 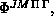 defined below, and calculated at the values
defined below, and calculated at the values
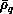 of
of 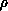 :
:
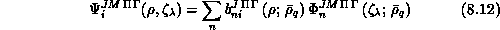
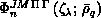 and
associated energies
and
associated energies 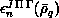 are,
respectively, the eigenfunctions and eigenvalues
of the surface Hamiltonian
are,
respectively, the eigenfunctions and eigenvalues
of the surface Hamiltonian 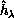 . They are obtained using
a variational approach [
. They are obtained using
a variational approach [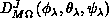 ,
associated Legendre functions of
,
associated Legendre functions of 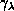 and functions of
and functions of
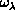 which depend parametically on
which depend parametically on 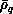 and are
obtained from the numerical solution of one-dimensional
eigenvalue-eigenfunction differential equations in
and are
obtained from the numerical solution of one-dimensional
eigenvalue-eigenfunction differential equations in 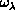 ,
involving a potential related to
,
involving a potential related to
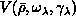 .
.
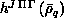 and
and
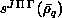 and whose elements are five-dimensional
integrals involving the variational basis functions.
and whose elements are five-dimensional
integrals involving the variational basis functions.
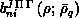 defined by
Equation
defined by
Equation 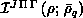 whose elements are defined
by
whose elements are defined
by
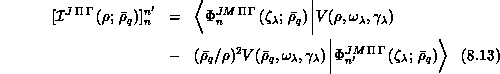
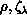 is divided into a set of Q
hyperspherical shells
is divided into a set of Q
hyperspherical shells 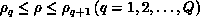 within each of which we choose a value
within each of which we choose a value 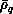 used in
expansion
used in
expansion 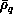 to the one at
to the one at
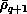 , neither
, neither 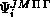 nor its derivative with
respect to
nor its derivative with
respect to 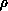 should change. This imposes continuity conditions on the
should change. This imposes continuity conditions on the
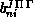 and their
and their 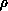 -derivatives at
-derivatives at 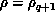 ,
involving the overlap matrix
,
involving the overlap matrix 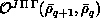 between the LHSF evaluated at
between the LHSF evaluated at 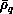 and
and
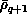
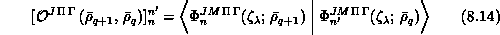
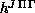 ,
, 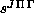 ,
, 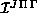 , and
, and
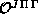 are performed analytically over
are performed analytically over 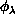 ,
,
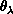 , and
, and 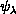 and by two-dimensional numerical
quadratures over
and by two-dimensional numerical
quadratures over 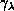 and
and 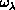 . These
quadratures account for 90% of the total time needed to calculate the LHSF
. These
quadratures account for 90% of the total time needed to calculate the LHSF
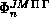 and the matrices
and the matrices 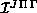 and
and
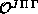 .
.
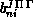 is integrated
as an initial value problem from small values of
is integrated
as an initial value problem from small values of 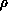 to large values
using Manolopoulos' logarithmic derivative propagator
[
to large values
using Manolopoulos' logarithmic derivative propagator
[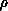 by a constant
by a constant 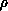 projection [
projection [