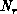 and
and 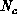 be the number of processors in the rows and columns of the
hypercube configuration, respectively. Element
be the number of processors in the rows and columns of the
hypercube configuration, respectively. Element 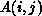 of an
of an 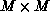 matrix is placed in processor row
matrix is placed in processor row 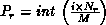 and column
and column 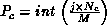 ,
where
,
where 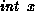 means the integer part of x.
means the integer part of x.





The computer used for this work is a 64-processor Mark IIIfp hypercube. The Crystalline Operating System (CrOS)-channel-addressed synchronous communication provides the library routines to handle communications between nodes [Fox:85d;85h;88a]. The programs are written in C programming language except for the time-consuming two-dimensional quadratures and matrix inversions, which are optimized in assembly language.
The hypercube was configured as a two-dimensional array of processors. The mapping is done using binary Gray codes [Gilbert:58a], [Fox:88a], [Salmon:84b], which gives the Cartesian coordinates in processor space and communication channel tags for a processor's nearest neighbors.
We mapped the matrices into processor space by local decomposition. Let
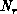 and
and 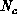 be the number of processors in the rows and columns of the
hypercube configuration, respectively. Element
be the number of processors in the rows and columns of the
hypercube configuration, respectively. Element 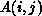 of an
of an 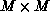 matrix is placed in processor row
matrix is placed in processor row 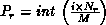 and column
and column 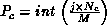 ,
where
,
where 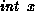 means the integer part of x.
means the integer part of x.
The parallel code implemented on the hypercube consists of five major steps.
Step one constructs, for each value of 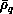 , a primitive basis set
composed of the product of Wigner rotation matrices, associated Legendre
functions, and the numerical one-dimensional functions in
, a primitive basis set
composed of the product of Wigner rotation matrices, associated Legendre
functions, and the numerical one-dimensional functions in 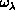 mentioned in Section 8.2.2 and obtained by solving the corresponding
one-dimensional eigenvalue-eigenvector differential equation using a finite
difference method. This requires that a subset of the eigenvalues and
eigenvectors of a tridiagonal matrix be found.
mentioned in Section 8.2.2 and obtained by solving the corresponding
one-dimensional eigenvalue-eigenvector differential equation using a finite
difference method. This requires that a subset of the eigenvalues and
eigenvectors of a tridiagonal matrix be found.
A bisection method [Fox:84g], [Ipsen:87a;87c], which accomplishes the eigenvalue computation using the TRIDIB routine from EISPACK [Smith:76a], was ported to the Mark IIIfp. This implementation of the bisection method allows computation of any number of consecutive eigenvalues specified by their indices. Eigenvectors are obtained using the EISPACK inverse iteration routine TINVIT with modified Gram-Schmidt orthogonalization. Each processor solves independent tridiagonal eigenproblems since the number of eigenvalues desired from each tridiagonal system is small, but there are a large number of distinct tridiagonal systems. To achieve load balancing, we distributed subsets of the primitive functions among the processors in such a way that no processor computes greater than one eigenvalue and eigenvector more than any other. These large grain tasks are most easily implemented on MIMD machines; SIMD (Single Instruction Multiple Data) machines would require more extensive modifications and would be less efficient because of the sequential nature of effective eigenvalue iteration procedures. The one-dimensional bases obtained are then broadcast to all the other nodes.
In step two, a large number of two-dimensional quadratures involving the primitive basis functions which are needed for the variational procedure are evaluated. These quadratures are highly parallel procedures requiring no communication overhead once each processor has the necessary subset of functions. Each processor calculates a subset of integrals independently.
Step three assembles these integrals into the real symmetric dense
matrices 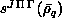 and
and
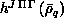 which are distributed over
processor space. The entire spectrum of eigenvalues and
eigenvectors for the associated
variational problem is sought. With the parallel implementation of the
Householder method [Fox:84h],
[Patterson:86a], this generalized eigensystem is tridiagonalized
and the resulting single tridiagonal matrix is solved completely in each processor with the QR
algorithm [Wilkinson:71a]. The QR
implementation is purely sequential since each processor obtains the
entire solution to the eigensystem. However, only different subsets of
the solution are kept in different processors for the evaluation of the
interaction and overlap matrices in step four. This part of the
algorithm is not time consuming and the straightforward sequential
approach was chosen. It has the further effect that the resulting
solutions are fully distributed, so no communication is required.
which are distributed over
processor space. The entire spectrum of eigenvalues and
eigenvectors for the associated
variational problem is sought. With the parallel implementation of the
Householder method [Fox:84h],
[Patterson:86a], this generalized eigensystem is tridiagonalized
and the resulting single tridiagonal matrix is solved completely in each processor with the QR
algorithm [Wilkinson:71a]. The QR
implementation is purely sequential since each processor obtains the
entire solution to the eigensystem. However, only different subsets of
the solution are kept in different processors for the evaluation of the
interaction and overlap matrices in step four. This part of the
algorithm is not time consuming and the straightforward sequential
approach was chosen. It has the further effect that the resulting
solutions are fully distributed, so no communication is required.
Step four evaluates the two-dimensional quadratures needed for the
interaction 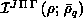 and
overlap
and
overlap 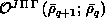 matrices. The same type of algorithms are used as in step two. By
far, the most expensive part of the sequential version of the surface
function calculation is the calculation of the large number of
two-dimensional numerical integrals required by steps two and four.
These steps are, however, highly parallel and well suited for the
hypercube.
matrices. The same type of algorithms are used as in step two. By
far, the most expensive part of the sequential version of the surface
function calculation is the calculation of the large number of
two-dimensional numerical integrals required by steps two and four.
These steps are, however, highly parallel and well suited for the
hypercube.
Step five uses Manolopoulos' [Manolopoulos:86a] algorithm to integrate
the coupled linear ordinary differential equations. The parallel
implementation of this algorithm is discussed elsewhere [Hipes:88b].
The algorithm is dominated by parallel Gauss-Jordan matrix inversion and is
I/O intensive, requiring the input of one interaction
matrix per integration step. To reduce the I/O overhead, a second
source of parallelism is exploited. The entire interaction matrix (at
all 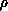 ) and overlap matrix (at all
) and overlap matrix (at all 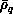 ) data sets are
loaded across the processors, and many collision energies are
calculated simultaneously. This strategy works because the same set of
data is used for each collision energy, and because enough main memory
is available. Calculation of scattering matrices from the final
logarithmic derivative matrices is not computationally intensive, and
is done sequentially.
) data sets are
loaded across the processors, and many collision energies are
calculated simultaneously. This strategy works because the same set of
data is used for each collision energy, and because enough main memory
is available. Calculation of scattering matrices from the final
logarithmic derivative matrices is not computationally intensive, and
is done sequentially.
The program steps were all run on the Weitek coprocessor, which only supports 32-bit arithmetic. Experimentation has shown that this precision is sufficient for the work reported below. The 64-bit arithmetic hardware needed for larger calculations was installed after the present calculations were completed.




