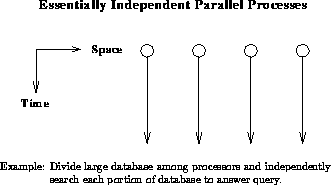
Figure 7.1: Embarrassingly Parallel Problem Class





In Chapters 4 and 6, we studied the synchronous problem class where the uniformity of the computation, that is, of the temporal structure, made the parallel implementation relatively straightforward. This chapter contains examples of the other major problem class, where the simple spatial structure leads to clear parallelization. We define the embarrassingly parallel class of problems for which the computational graph is disconnected. This spatial structure allows a simple parallelization as no (temporal) synchronization is involved. In Chapters 4 and 6, on the other hand, there was often substantial synchronization and associated communication; however, the uniformity of the synchronization allowed a clear parallelization strategy. One important feature of embarrassingly parallel problems is the modest node-to-node communication requirements-the definition of no spatial connection implies in fact no internode communication, but a practical problem would involve some amount of communication, if only to set up the problem and accumulate results. The low communication requirements of embarrassingly parallel problems make them particularly suitable for a distributed computing implementation on a network of workstations; even the low bandwidth of an Ethernet is often sufficient. Indeed, we used such a network of Sun workstations to support some of the simulations described in Section 7.2.
The caricature of this problem class, shown in Figure 7.1, uses a database problem as an example. This is illustrated in practice by the DOWQUEST program where a CM-2 supports searching of financial data contained in articles that are partitioned equally over the nodes of this SIMD machine [Waltz:87a;88a,90a].

Figure 7.1: Embarrassingly Parallel Problem Class
This problem class can have either a synchronous or asynchronous
temporal structure. We have illustrated the
former above and analysis of a large (high energy) physics data set
exhibits asynchronous temporal structure. Such experiments can record
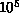 -
-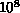 separate events, which can be analyzed independently.
However, each event is usually quite different and would require both
distinct instruction streams and very different execution times. This
was realized early in the high energy physics community and so-called farms-initially of special-purpose
machines and now of commercial workstations-have been used
extensively for production data analysis
[Gaines:87a], [Hey:88a], [Kunz:81a].
separate events, which can be analyzed independently.
However, each event is usually quite different and would require both
distinct instruction streams and very different execution times. This
was realized early in the high energy physics community and so-called farms-initially of special-purpose
machines and now of commercial workstations-have been used
extensively for production data analysis
[Gaines:87a], [Hey:88a], [Kunz:81a].
The applications in Sections 7.2 and 7.6 obtain their
embarrassingly parallel structure from running several full
simulations-each with independent data. Each simulation could in
fact also be decomposed spatially and in fact this spatial
parallelization has since been pursued and is described for the neural
network simulator in Section 7.6. Some of Chiu's random block
lattice calculations also used an embarrassingly parallel approach with
1024 separate 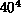 lattices being calculated on the 1024
nCUBE-1 at Sandia [Chiu:90a],
[Fox:89i;89n]. This would not, of course, be possible
for the QCD of Section 4.3, where each node would not be
available to hold an interesting size lattice. The spatial parallelism
in the examples of Sections 7.2 and 7.6 is nontrivial
to implement as the irregularities makes these problems loosely
synchronous. This relatively difficult domain parallelism made it
attractive to first explore the independent structure gotten by
exploiting the parallelism coming from simulations with different
parameters.
lattices being calculated on the 1024
nCUBE-1 at Sandia [Chiu:90a],
[Fox:89i;89n]. This would not, of course, be possible
for the QCD of Section 4.3, where each node would not be
available to hold an interesting size lattice. The spatial parallelism
in the examples of Sections 7.2 and 7.6 is nontrivial
to implement as the irregularities makes these problems loosely
synchronous. This relatively difficult domain parallelism made it
attractive to first explore the independent structure gotten by
exploiting the parallelism coming from simulations with different
parameters.
It is interesting that Sections 6.3 and 7.3 both
address simulations of spin systems relevant to high 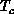 -depending
on the algorithm used, one can get very different problem
architectures (either synchronous or
embarrassingly parallel in this case) for a given application.
-depending
on the algorithm used, one can get very different problem
architectures (either synchronous or
embarrassingly parallel in this case) for a given application.
The embarrassingly parallel gravitational lens application of Section 7.4 was frustrating for the developers as it needed software support not available at the time on the Mark III. Suitable software (MOOSE in Section 15.2) had been developed on the Mark II to support graphics ray tracing as briefly discussed in Section 14.1. Thus, the calculation is embarrassingly parallel, but a distributed database is essentially needed to support the calculation of each ray. This was not available in CrOS III at the time of the calculations described in Section 7.4.




