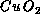 planes, perhaps through the formation
of bound hole pairs. In the undoped materials (``precursor
insulators''), these
planes, perhaps through the formation
of bound hole pairs. In the undoped materials (``precursor
insulators''), these 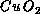 planes are magnetic insulators and
appear to be well described by the two-dimensional spin-1/2 Heisenberg
antiferromagnet,
planes are magnetic insulators and
appear to be well described by the two-dimensional spin-1/2 Heisenberg
antiferromagnet,





Although the mechanism of high-temperature
superconductivity is not yet established, an enormous
amount of experimental work has been completed on these materials and, as a
result, a ``magnetic'' explanation has probably gained
the largest number of adherents. In this picture, high-temperature
superconductivity results from the effects of dynamical holes on the
magnetic properties of 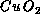 planes, perhaps through the formation
of bound hole pairs. In the undoped materials (``precursor
insulators''), these
planes, perhaps through the formation
of bound hole pairs. In the undoped materials (``precursor
insulators''), these 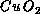 planes are magnetic insulators and
appear to be well described by the two-dimensional spin-1/2 Heisenberg
antiferromagnet,
planes are magnetic insulators and
appear to be well described by the two-dimensional spin-1/2 Heisenberg
antiferromagnet,
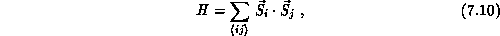
where each spin represents a d-electron on a 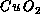 site. Since many
aspects of the two-dimensional Heisenberg antiferromagnet were obscure before
the discovery of high-T
site. Since many
aspects of the two-dimensional Heisenberg antiferromagnet were obscure before
the discovery of high-T , this model has been the subject of intense
numerical study, and comparisons with experiments on the precursor insulators
have generally been successful. (A review of this subject including recent
references has been prepared for the
, this model has been the subject of intense
numerical study, and comparisons with experiments on the precursor insulators
have generally been successful. (A review of this subject including recent
references has been prepared for the  group [Barnes:91a].) If
the proposed ``magnetic'' origin of high-temperature superconductivity is
correct, one may only need to incorporate dynamical holes in the Heisenberg
antiferromagnet to construct a model that exhibits high-temperature
superconductivity. Unfortunately, such models (for example, the ``t-J''
model) are dynamical many-fermion systems and exhibit the ``minus sign
problem'' which makes them very difficult to simulate on large lattices
using Monte Carlo techniques. The lack of appropriate algorithms for
many-fermion systems accounts in large part for the uncertainty in the
predictions of these models.
group [Barnes:91a].) If
the proposed ``magnetic'' origin of high-temperature superconductivity is
correct, one may only need to incorporate dynamical holes in the Heisenberg
antiferromagnet to construct a model that exhibits high-temperature
superconductivity. Unfortunately, such models (for example, the ``t-J''
model) are dynamical many-fermion systems and exhibit the ``minus sign
problem'' which makes them very difficult to simulate on large lattices
using Monte Carlo techniques. The lack of appropriate algorithms for
many-fermion systems accounts in large part for the uncertainty in the
predictions of these models.
In our work, we carried out numerical simulations of the low-lying states of
one- and two-dimensional Heisenberg antiferromagnets; the problems we studied
on the hypercube which relate to high-T systems were the determination of
low-lying energies and ground state matrix elements of the two-dimensional
spin-1/2 Heisenberg antiferromagnet, and in particular the response of the
ground state to anisotropic couplings in the generalized model
systems were the determination of
low-lying energies and ground state matrix elements of the two-dimensional
spin-1/2 Heisenberg antiferromagnet, and in particular the response of the
ground state to anisotropic couplings in the generalized model
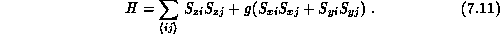
Until recently, the possible existence of infinite-range spin
antialignment ``staggered magnetization'' in the ground state of the
two-dimensional Heisenberg antiferromagnet, which would imply
spontaneous breaking of rotational symmetry, was considered an open
question. Since the precursor insulators such as 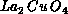 are
observed to have a nonzero staggered magnetization, one might hope to
observe it in the Heisenberg model as well. (It has actually been
proven to be zero in the isotropic model above zero temperature, so
this is a very delicate kind of long-range order.) Assuming that such
order exists, one might expect to see various kinds of singular
behavior in response to anisotropies, which would choose a preferred
direction for symmetry breaking in the ground state. In our numerical
simulations we measured the ground state energy per spin
are
observed to have a nonzero staggered magnetization, one might hope to
observe it in the Heisenberg model as well. (It has actually been
proven to be zero in the isotropic model above zero temperature, so
this is a very delicate kind of long-range order.) Assuming that such
order exists, one might expect to see various kinds of singular
behavior in response to anisotropies, which would choose a preferred
direction for symmetry breaking in the ground state. In our numerical
simulations we measured the ground state energy per spin 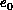 , the
energy gap to the first spin excitation
, the
energy gap to the first spin excitation 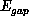 , and the
, and the  component of the staggered magnetization N
component of the staggered magnetization N , as a function of the
anisotropy parameter g on L
, as a function of the
anisotropy parameter g on L L square lattices, extrapolated to
the bulk limit. We did indeed find evidence of singular behavior at
the isotropic point g=1, specifically that
L square lattices, extrapolated to
the bulk limit. We did indeed find evidence of singular behavior at
the isotropic point g=1, specifically that 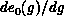 is probably
discontinuous there (Figure 7.8),
is probably
discontinuous there (Figure 7.8), 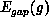 decreases to
zero at g=1 (Figure 7.9) and remains zero for g>1, and
N
decreases to
zero at g=1 (Figure 7.9) and remains zero for g>1, and
N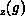 decreases to a nonzero limit as g approaches one, is zero
for g>1, and is undefined at g=1
([Barnes:89a;89c]). Finite lattice results which
led to this conclusion are shown in Figure 7.10.
(Perturbative and spin-wave predictions also appear in these figures;
details are discussed in the publications we have cited.) These
results are consistent with a ``spin flop'' transition, in which the
long-range spin order is oriented along the energetically most
favorable direction, which changes discontinuously from
decreases to a nonzero limit as g approaches one, is zero
for g>1, and is undefined at g=1
([Barnes:89a;89c]). Finite lattice results which
led to this conclusion are shown in Figure 7.10.
(Perturbative and spin-wave predictions also appear in these figures;
details are discussed in the publications we have cited.) These
results are consistent with a ``spin flop'' transition, in which the
long-range spin order is oriented along the energetically most
favorable direction, which changes discontinuously from  to
planar as g passes through the isotropic point. The qualitative
behavior of the energy gap can be understood as a consequence of
Goldstone's theorem, given these types of spontaneous symmetry
breaking. Our results also provided interesting tests of spin-wave
theory, which has been applied to the study of many antiferromagnetic
systems including the two-dimensional Heisenberg model, but is of
questionable accuracy for small spin. In this spin-1/2 case, we found
that finite-size and anisotropic effects were qualitatively described
surprisingly well by spin-wave theory, but that actual numerical values
were sometimes rather inaccurate; for example, the energy gap due to
a small easy-axis anisotropy was in error by about a factor of two.
to
planar as g passes through the isotropic point. The qualitative
behavior of the energy gap can be understood as a consequence of
Goldstone's theorem, given these types of spontaneous symmetry
breaking. Our results also provided interesting tests of spin-wave
theory, which has been applied to the study of many antiferromagnetic
systems including the two-dimensional Heisenberg model, but is of
questionable accuracy for small spin. In this spin-1/2 case, we found
that finite-size and anisotropic effects were qualitatively described
surprisingly well by spin-wave theory, but that actual numerical values
were sometimes rather inaccurate; for example, the energy gap due to
a small easy-axis anisotropy was in error by about a factor of two.
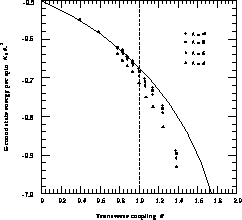
Figure 7.8: Ground State Energy per Spin
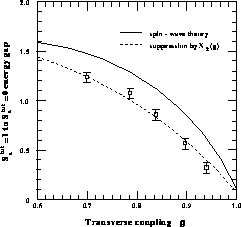
Figure 7.9: Spin Excitation Energy Gap
In related work, we developed hypercube programs to study static holes in
the Heisenberg model, as a first step towards more general Monte Carlo
investigations of the behavior of holes in antiferromagnets.
Preliminary static-hole results have been published [Barnes:90b],
and our collaboration is now continuing to study high-T models on an
Intel iPSC/860 hypercube at Oak Ridge National Laboratory.
models on an
Intel iPSC/860 hypercube at Oak Ridge National Laboratory.
For our studies on the Caltech machine, we used the DGRW (discrete guided
random-walk) Monte Carlo algorithm [Barnes:88c],
and incorporated algorithm improvements which lowered the statistical
errors [Barnes:89b]. This algorithm solves the Euclidean time
Schrödinger equation stochastically by running random walks in the
configuration space of the system and accumulating a weight factor,
which implicitly contains energies and matrix elements. Since the
algorithm only requires a single configuration, our memory requirements
were very small, and we simply placed a copy of the program on each
node; no internode communication was necessary. A previously
developed DGRW spin system Fortran program written by T. Barnes was
rewritten in C and adapted to the hypercube by D. Kotchan, and an
independent DGRW code was written by E. S. Swanson for
debugging purposes. Our collaboration for this work
eventually grew to include K. J. Cappon (who also wrote a DGRW Monte
Carlo code) and E. Dagotto (UCSB/ITP) and A. Moreo (UCSB), who wrote
Lanczos programs to give essentially exact results on the 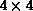 lattice. This provided an independent check of the accuracy of our
Monte Carlo results.
lattice. This provided an independent check of the accuracy of our
Monte Carlo results.
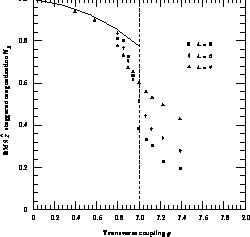
Figure 7.10: Ground State Staggered Magnetization 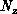
In addition to providing resources that led to these physics results,
access to the hypercube and the support of the  group were
very helpful in the PhD programs of D. Kotchan and E. S. Swanson, and
their experience has encouraged several other graduate-level theorists
at the University of Toronto to pursue studies in computational
physics, in the areas of high-temperature superconductivity
(K. J. Cappon and W. MacReady) and Monte Carlo studies of quark model
physics (G. Grondin).
group were
very helpful in the PhD programs of D. Kotchan and E. S. Swanson, and
their experience has encouraged several other graduate-level theorists
at the University of Toronto to pursue studies in computational
physics, in the areas of high-temperature superconductivity
(K. J. Cappon and W. MacReady) and Monte Carlo studies of quark model
physics (G. Grondin).




