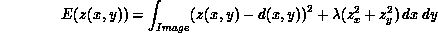
For the surface reconstruction problem (see [Terzopoulos:86a]) the energy functional is:
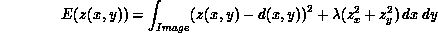
A physical analogy is that of fitting the depth constraints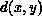 
with a
membrane pulled by springs connected to them. The effect of active
discontinuities 
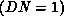is that of ``cutting the membrane'' in the proper
places.
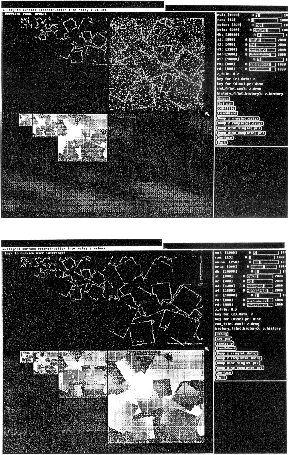
Figure 6.28: Simulation Environment for Multigrid Surface Reconstruction
from a Noisy Image. The top screen shows an intermediate, and the
bottom final results. For each screen, the upper part displays the activated
discontinuities; the lower part, the gray-encoded z values of the
surface.
Figure 6.29: The Original Surface (top) and Surface Corrupted by 25%
Noise (bottom)
Figure 6.30: The Reconstruction of a ``Randomville'' Scenery using
Multigrid Method. Each figure shows a different resolution.
Figure 6.28 to 6.30 show the simulation environment on the SUN workstation, and the reconstruction of a ``Randomville'' image (random quadrangular blocks placed in the image plane). The original surface, the surface corrupted by noise (25%), are shown in Figure 6.29 while reconstruction on different scales is shown in Figure 6.30.
For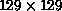 
``images'' and 25% noise, a faithful reconstruction of
the surface (within a few percent of the original one) is obtained after a
single multiscale sweep (with V cycles) on four layers. The total
computational time corresponds approximately to the time required by three
relaxations on the finest grid. Because of the optimality of multiscale
methods, time increases linearly with the number of image pixels.