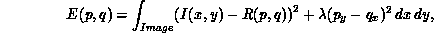
An iterative scheme for solving the shape from shading problem has been proposed in [Horn:85a]. A preliminary phase recovers information about orientation of the planes tangent to the surface at each point by minimizing a functional containing the image irradiance equation and an integrability constraint, as follows:
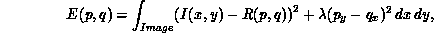
where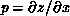 
, 
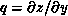, I =
measured intensity, and R = theoretical reflectance function.
After the tangent planes are available, the surface z is reconstructed, minimizing the following functional:
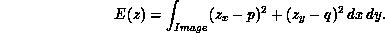
Euler-Lagrange differential equations and discretization are left as an exercise to the reader.
Figure 6.26 shows the reconstruction of the shape of a
hemispherical surface starting from a ray-traced image 
. Left is the result of standard
relaxation after 100 sweeps, right the ``minimal multigrid'' result (with
computation time equivalent to 3 to 4 sweeps at the finest resolution).
Figure 6.26: Reconstruction of Shape From Shading: Standard Relaxation
(top right) Versus Multigrid (bottom right). The original image is
shown on left.
This case is particularly hard for a standard relaxation approach. The image can be interpreted ``legally'' in two possible ways, as either a concave or convex hemisphere. Starting from random initial values, after some relaxations, some image patches typically ``vote'' for one or the other interpretation and try to extend the local interpretation to a global one. This is slow (given the local nature of the updating rule) and encounters an endless struggle in the regions that mark the border between different interpretations. The multigrid approach solves this ``democratic impasse'' on the coarsest grids (much faster because information spreads over large distances) and propagates this decision to the finer grids, that will now concentrate their efforts on refining the initial approximation.
In Figure 6.27, we show the reconstruction of the Mona Lisa face painted by Leonardo da Vinci.
Figure 6.27: Mona Lisa in Three Dimensions. The right figure shows the
multigrid reconstruction.