The starting point for an incomplete block factorization is a
partitioning of the matrix, as mentioned in §![]() .
Then an incomplete factorization is performed using the matrix blocks
as basic entities (see Axelsson [12] and Concus, Golub
and Meurant [57] as
basic references).
.
Then an incomplete factorization is performed using the matrix blocks
as basic entities (see Axelsson [12] and Concus, Golub
and Meurant [57] as
basic references).
The most important difference with point methods arises in the inversion of the pivot blocks. Whereas inverting a scalar is easily done, in the block case two problems arise. First, inverting the pivot block is likely to be a costly operation. Second, initially the diagonal blocks of the matrix are likely to be be sparse and we would like to maintain this type of structure throughout the factorization. Hence the need for approximations of inverses arises.

Figure: Block version of a 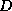 -
-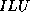 factorization
factorization
In addition to this, often fill-in in off-diagonal blocks is discarded
altogether. Figure ![]() describes an incomplete block
factorization that is analogous to the
describes an incomplete block
factorization that is analogous to the 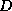 -
-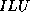 factorization
(section
factorization
(section ![]() ) in that it only updates the diagonal blocks.
) in that it only updates the diagonal blocks.
As in the case of incomplete point factorizations, the existence of
incomplete block methods is guaranteed if the coefficient
matrix is an  -matrix. For a general proof, see
Axelsson [13].
-matrix. For a general proof, see
Axelsson [13].