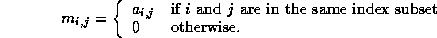Block Jacobi Methods





Next: Discussion
Up: Jacobi Preconditioning
Previous: Jacobi Preconditioning
Block versions of the Jacobi preconditioner can be derived by a
partitioning of the variables. If the index set 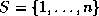 is partitioned as
is partitioned as 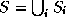 with the sets
with the sets 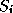 mutually
disjoint, then
mutually
disjoint, then
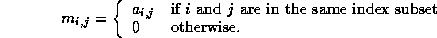
The preconditioner is now a block-diagonal matrix.
Often, natural choices for the partitioning suggest themselves:
- In problems with multiple physical variables per node,
blocks can be formed by grouping the equations per node.
- In structured matrices, such as those from partial differential
equations on regular grids, a partitioning can be based on the
physical domain. Examples are a partitioning along lines in the
2D case, or planes in the 3D case. This will be discussed
further in §
 .
.
- On parallel computers it is natural to let the
partitioning coincide with the division of variables
over the processors.
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
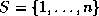 is partitioned as
is partitioned as 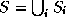 with the sets
with the sets 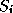 mutually
disjoint, then
mutually
disjoint, then
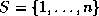 is partitioned as
is partitioned as 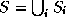 with the sets
with the sets 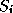 mutually
disjoint, then
mutually
disjoint, then