Overview





Next: Balancing and Conditioning
Up: Further Details: Error
Previous: Further Details: Error
In this subsection, we will summarize all the available error bounds.
Later subsections will provide further details. The reader may also
refer to [11].
Bounds for individual eigenvalues and eigenvectors are provided by
driver xGEEVX (subsection 2.2.4) or computational
routine xTRSNA (subsection 2.3.5).
Bounds for
clusters of eigenvalues
and their associated invariant subspace are
provided by driver xGEESX (subsection 2.2.4) or
computational routine xTRSEN (subsection 2.3.5).
We let 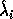 be the i-th computed eigenvalue and
be the i-th computed eigenvalue and
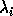 an i-th true eigenvalue.
an i-th true eigenvalue. Let
Let 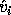 be the
corresponding computed right eigenvector, and
be the
corresponding computed right eigenvector, and 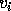 a true right
eigenvector (so
a true right
eigenvector (so 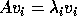 ).
If
).
If 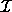 is a subset of the
integers from 1 to n, we let
is a subset of the
integers from 1 to n, we let 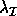 denote the average of
the selected eigenvalues:
denote the average of
the selected eigenvalues:
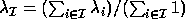 ,
and similarly for
,
and similarly for 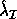 . We also let
. We also let 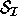 denote the subspace spanned by
denote the subspace spanned by 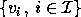 ; it is
called a right invariant subspace because if v is any vector in
; it is
called a right invariant subspace because if v is any vector in 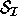 then
Av is also in
then
Av is also in 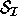 .
. 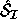 is the corresponding computed subspace.
is the corresponding computed subspace.
The algorithms for the nonsymmetric eigenproblem are normwise backward stable:
they compute the exact eigenvalues, eigenvectors and invariant subspaces
of slightly perturbed matrices A + E, where 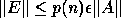 .
Some of the bounds are stated in terms of
.
Some of the bounds are stated in terms of  and others in
terms of
and others in
terms of 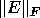 ; one may use
; one may use 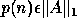 to approximate
either quantity.
The code fragment in the previous subsection approximates
to approximate
either quantity.
The code fragment in the previous subsection approximates
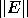 by
by  , where
, where 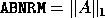 is returned by xGEEVX.
is returned by xGEEVX.
xGEEVX (or xTRSNA) returns two quantities for each
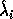 ,
, 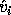 pair:
pair: 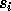 and
and  .
xGEESX (or xTRSEN) returns two quantities for a selected subset
.
xGEESX (or xTRSEN) returns two quantities for a selected subset
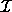 of eigenvalues:
of eigenvalues: 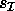 and
and 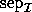 .
.
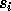 (or
(or 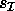 ) is a reciprocal condition number for the
computed eigenvalue
) is a reciprocal condition number for the
computed eigenvalue 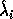 (or
(or 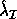 ),
and is referred to as RCONDE by xGEEVX (or xGEESX).
),
and is referred to as RCONDE by xGEEVX (or xGEESX).
 (or
(or 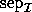 ) is a reciprocal condition number for
the right eigenvector
) is a reciprocal condition number for
the right eigenvector 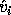 (or
(or 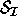 ), and
is referred to as RCONDV by xGEEVX (or xGEESX).
The approximate error bounds for eigenvalues, averages of eigenvalues,
eigenvectors, and invariant subspaces
provided in Table 4.5 are
true for sufficiently small ||E||, which is why they are called asymptotic.
), and
is referred to as RCONDV by xGEEVX (or xGEESX).
The approximate error bounds for eigenvalues, averages of eigenvalues,
eigenvectors, and invariant subspaces
provided in Table 4.5 are
true for sufficiently small ||E||, which is why they are called asymptotic.
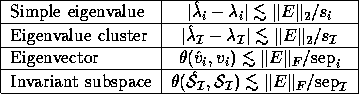
Table 4.5: Asymptotic error bounds for the nonsymmetric eigenproblem
If the problem is ill-conditioned, the asymptotic bounds may only hold
for extremely small ||E||. Therefore, in Table 4.6
we also provide global bounds
which are guaranteed to hold for all 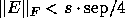 .
.

Table 4.6: Global error bounds for the nonsymmetric eigenproblem
assuming 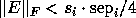
We also have the following bound, which is true for all E:
all the 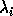 lie in the union of n disks,
where the i-th disk is centered at
lie in the union of n disks,
where the i-th disk is centered at 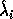 and has
radius
and has
radius 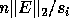 . If k of these disks overlap,
so that any two points inside the k disks can be connected
by a continuous curve lying entirely inside the k disks,
and if no larger set of k + 1 disks has this property,
then exactly k of the
. If k of these disks overlap,
so that any two points inside the k disks can be connected
by a continuous curve lying entirely inside the k disks,
and if no larger set of k + 1 disks has this property,
then exactly k of the 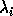 lie inside the
union of these k disks. Figure 4.1 illustrates
this for a 10-by-10 matrix, with 4 such overlapping unions
of disks, two containing 1 eigenvalue each, one containing 2
eigenvalues, and one containing 6 eigenvalues.
lie inside the
union of these k disks. Figure 4.1 illustrates
this for a 10-by-10 matrix, with 4 such overlapping unions
of disks, two containing 1 eigenvalue each, one containing 2
eigenvalues, and one containing 6 eigenvalues.
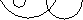
Figure 4.1: Bounding eigenvalues inside overlapping disks
Finally, the quantities s and sep tell use how we can best
(block) diagonalize a matrix A by a similarity,
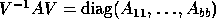 , where each diagonal block
, where each diagonal block
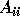 has a selected subset of the eigenvalues of A. Such a decomposition
may be useful in computing functions of matrices, for example.
The goal is to choose a V with a nearly minimum condition number
has a selected subset of the eigenvalues of A. Such a decomposition
may be useful in computing functions of matrices, for example.
The goal is to choose a V with a nearly minimum condition number
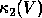 which performs this decomposition, since this generally minimizes the error
in the decomposition.
This may be done as follows. Let
which performs this decomposition, since this generally minimizes the error
in the decomposition.
This may be done as follows. Let 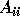 be
be
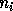 -by-
-by-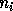 . Then columns
. Then columns  through
through
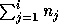 of V span the invariant
subspace of A corresponding
to the eigenvalues of
of V span the invariant
subspace of A corresponding
to the eigenvalues of 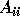 ; these columns should be chosen to be any
orthonormal basis of this space (as computed by xGEESX, for example).
Let
; these columns should be chosen to be any
orthonormal basis of this space (as computed by xGEESX, for example).
Let 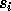 be the value corresponding to the
cluster of
eigenvalues of
be the value corresponding to the
cluster of
eigenvalues of 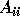 , as computed by xGEESX or xTRSEN. Then
, as computed by xGEESX or xTRSEN. Then
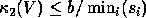 , and no other choice of V can make
its condition number smaller than
, and no other choice of V can make
its condition number smaller than 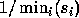 [17].
Thus choosing orthonormal
subblocks of V gets
[17].
Thus choosing orthonormal
subblocks of V gets 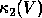 to within a factor b of its minimum
value.
to within a factor b of its minimum
value.
In the case of a real symmetric (or complex Hermitian) matrix,
s = 1 and sep is the absolute gap, as defined in subsection 4.7.
The bounds in Table 4.5 then reduce to the
bounds in subsection 4.7.





Next: Balancing and Conditioning
Up: Further Details: Error
Previous: Further Details: Error
Tue Nov 29 14:03:33 EST 1994
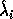 be the i-th computed eigenvalue and
be the i-th computed eigenvalue and
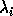 an i-th true eigenvalue.
an i-th true eigenvalue.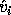 be the
corresponding computed right eigenvector, and
be the
corresponding computed right eigenvector, and 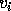 a true right
eigenvector (so
a true right
eigenvector (so 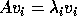 ).
If
).
If 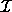 is a subset of the
integers from 1 to n, we let
is a subset of the
integers from 1 to n, we let 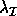 denote the average of
the selected eigenvalues:
denote the average of
the selected eigenvalues:
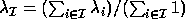 ,
and similarly for
,
and similarly for 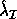 . We also let
. We also let 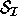 denote the subspace spanned by
denote the subspace spanned by 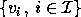 ; it is
called a right invariant subspace because if v is any vector in
; it is
called a right invariant subspace because if v is any vector in 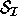 then
Av is also in
then
Av is also in 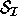 .
. 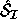 is the corresponding computed subspace.
is the corresponding computed subspace.
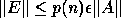 .
Some of the bounds are stated in terms of
.
Some of the bounds are stated in terms of  and others in
terms of
and others in
terms of 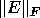 ; one may use
; one may use 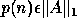 to approximate
either quantity.
The code fragment in the previous subsection approximates
to approximate
either quantity.
The code fragment in the previous subsection approximates
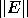 by
by 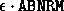 , where
, where 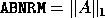 is returned by xGEEVX.
is returned by xGEEVX.
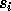 and
and  .
xGEESX (or xTRSEN) returns two quantities for a selected subset
.
xGEESX (or xTRSEN) returns two quantities for a selected subset
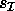 and
and 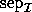 .
.
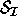 ), and
is referred to as RCONDV by xGEEVX (or xGEESX).
), and
is referred to as RCONDV by xGEEVX (or xGEESX).
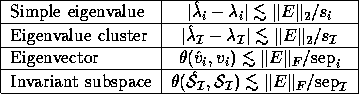
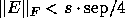 .
.

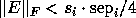
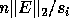 . If k of these disks overlap,
so that any two points inside the k disks can be connected
by a continuous curve lying entirely inside the k disks,
and if no larger set of k + 1 disks has this property,
then exactly k of the
. If k of these disks overlap,
so that any two points inside the k disks can be connected
by a continuous curve lying entirely inside the k disks,
and if no larger set of k + 1 disks has this property,
then exactly k of the 
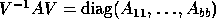 , where each diagonal block
, where each diagonal block
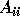 has a selected subset of the eigenvalues of A. Such a decomposition
may be useful in computing functions of matrices, for example.
The goal is to choose a V with a nearly minimum condition number
has a selected subset of the eigenvalues of A. Such a decomposition
may be useful in computing functions of matrices, for example.
The goal is to choose a V with a nearly minimum condition number
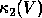
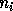 -by-
-by- through
through
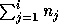 of V span the invariant
subspace
of V span the invariant
subspace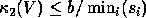 , and no other choice of V can make
its condition number smaller than
, and no other choice of V can make
its condition number smaller than