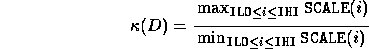Balancing and Conditioning





Next: Computing and
Up: Further Details: Error
Previous: Overview
There are two preprocessing
steps one may perform
on a matrix A in order
to make its eigenproblem easier. The first is permutation, or
reordering the rows and columns to make A more nearly upper triangular
(closer to Schur form): 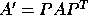 , where P is a permutation matrix.
If
, where P is a permutation matrix.
If 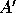 is permutable to upper triangular form (or close to it), then
no floating-point operations (or very few) are needed to reduce it to
Schur form.
The second is scaling by a diagonal matrix D to make the rows and
columns of
is permutable to upper triangular form (or close to it), then
no floating-point operations (or very few) are needed to reduce it to
Schur form.
The second is scaling by a diagonal matrix D to make the rows and
columns of 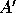 more nearly equal in norm:
more nearly equal in norm: 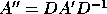 . Scaling
can make the matrix norm smaller with respect to the eigenvalues, and so
possibly reduce the inaccuracy contributed by roundoff
[][Chap. II/11]wilkinson3. We refer to these two operations as
.
. Scaling
can make the matrix norm smaller with respect to the eigenvalues, and so
possibly reduce the inaccuracy contributed by roundoff
[][Chap. II/11]wilkinson3. We refer to these two operations as
.
Balancing is performed by driver xGEEVX, which calls
computational routine xGEBAL. The user may tell xGEEVX to optionally
permute, scale, do both, or do neither; this is specified by input
parameter BALANC. Permuting has no effect on
the condition numbers
or their interpretation as described in previous
subsections. Scaling, however, does change their interpretation,
as we now describe.
The output parameters of xGEEVX - SCALE (real array of length N),
ILO (integer), IHI (integer) and ABNRM (real) - describe
the result of
balancing a matrix A into 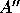 , where N is the dimension of A.
The matrix
, where N is the dimension of A.
The matrix 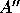 is block upper triangular, with at most three blocks:
from 1 to ILO - 1, from ILO to IHI, and from IHI + 1 to N.
The first and last blocks are upper triangular, and so already in Schur
form. These are not scaled; only the block from ILO to IHI is scaled.
Details of the scaling and permutation are described in SCALE (see the
specification of xGEEVX or xGEBAL for details) . The one-norm of
is block upper triangular, with at most three blocks:
from 1 to ILO - 1, from ILO to IHI, and from IHI + 1 to N.
The first and last blocks are upper triangular, and so already in Schur
form. These are not scaled; only the block from ILO to IHI is scaled.
Details of the scaling and permutation are described in SCALE (see the
specification of xGEEVX or xGEBAL for details) . The one-norm of
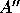 is returned in ABNRM.
is returned in ABNRM.
The condition numbers
described in earlier subsections are computed for
the balanced matrix 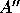 , and so some interpretation is needed to
apply them to the eigenvalues and eigenvectors of the original matrix A.
To use the bounds for eigenvalues in Tables 4.5 and
4.6,
we must replace
, and so some interpretation is needed to
apply them to the eigenvalues and eigenvectors of the original matrix A.
To use the bounds for eigenvalues in Tables 4.5 and
4.6,
we must replace  and
and 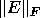 by
by  . To use the
bounds for eigenvectors, we also need to take into account that bounds
on rotations of eigenvectors are for the eigenvectors
. To use the
bounds for eigenvectors, we also need to take into account that bounds
on rotations of eigenvectors are for the eigenvectors  of
of
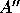 , which are related to the eigenvectors x of A by
, which are related to the eigenvectors x of A by
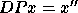 , or
, or 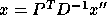 . One coarse but simple way to do this is
as follows: let
. One coarse but simple way to do this is
as follows: let 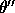 be the bound on rotations of
be the bound on rotations of  from
Table 4.5 or Table 4.6
and let
from
Table 4.5 or Table 4.6
and let  be the desired bound on rotation of x. Let
be the desired bound on rotation of x. Let
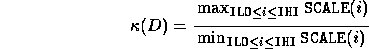
be the condition number of D.
Then

The numerical example in subsection 4.8 does no scaling,
just permutation.





Next: Computing and
Up: Further Details: Error
Previous: Overview
Tue Nov 29 14:03:33 EST 1994
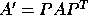 , where P is a permutation matrix.
If
, where P is a permutation matrix.
If 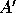 is permutable to upper triangular form (or close to it), then
no floating-point operations (or very few) are needed to reduce it to
Schur form.
The second is scaling by a diagonal matrix D to make the rows and
columns of
is permutable to upper triangular form (or close to it), then
no floating-point operations (or very few) are needed to reduce it to
Schur form.
The second is scaling by a diagonal matrix D to make the rows and
columns of 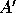 more nearly equal in norm:
more nearly equal in norm: 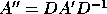 . Scaling
can make the matrix norm smaller with respect to the eigenvalues, and so
possibly reduce the inaccuracy contributed by roundoff
[][Chap. II/11]wilkinson3. We refer to these two operations as
.
. Scaling
can make the matrix norm smaller with respect to the eigenvalues, and so
possibly reduce the inaccuracy contributed by roundoff
[][Chap. II/11]wilkinson3. We refer to these two operations as
.
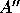 , where N is the dimension of A.
The matrix
, where N is the dimension of A.
The matrix  and
and 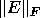 by
by  . To use the
bounds for eigenvectors, we also need to take into account that bounds
on rotations of eigenvectors are for the eigenvectors
. To use the
bounds for eigenvectors, we also need to take into account that bounds
on rotations of eigenvectors are for the eigenvectors  of
of
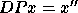 , or
, or 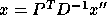 . One coarse but simple way to do this is
as follows: let
. One coarse but simple way to do this is
as follows: let 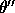 be the bound on rotations of
be the bound on rotations of  be the desired bound on rotation of x. Let
be the desired bound on rotation of x. Let