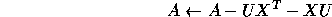
using the Level 3 BLAS routine SSYR2K; Level 3 BLAS account for at most half the work.
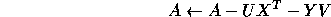
using two calls to the Level 3 BLAS routine SGEMM; Level 3 BLAS account for at most half the work.
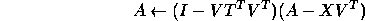
Level 3 BLAS account for at most three-quarters of the work.
Eigenvalue problems have until recently provided a less fertile ground for the development of block algorithms than the factorizations so far described. Version 2.0 of LAPACK includes new block algorithms for the symmetric eigenvalue problem, and future releases will include analogous algorithms for the singular value decomposition.
The first step in solving many types of eigenvalue problems is to reduce the original matrix to a ``condensed form'' by orthogonal transformations .
In the reduction to condensed forms, the unblocked algorithms all use elementary Householder matrices and have good vector performance. Block forms of these algorithms have been developed [34], but all require additional operations, and a significant proportion of the work must still be performed by Level 2 BLAS, so there is less possibility of compensating for the extra operations.
The algorithms concerned are:
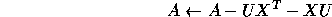
using the Level 3 BLAS routine SSYR2K; Level 3 BLAS account for at most half the work.
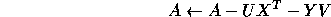
using two calls to the Level 3 BLAS routine SGEMM; Level 3 BLAS account for at most half the work.
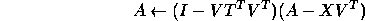
Level 3 BLAS account for at most three-quarters of the work.
Note that only in the reduction to Hessenberg form is it possible to use the block Householder representation described in subsection 3.4.2. Extra work must be performed to compute the n-by-b matrices X and Y that are required for the block updates (b is the block size) - and extra workspace is needed to store them.
Nevertheless, the performance gains can be worthwhile on some machines, for example, on an IBM POWER2 model 590, as shown in Table 3.7.
(all matrices are square of order n)
----------------------------
Block Values of n
size 100 1000
----------------------------
DSYTRD 1 137 159
16 82 169
----------------------------
DGEBRD 1 90 110
16 90 136
----------------------------
DGEHRD 1 111 113
16 125 187
----------------------------
Table 3.7: Speed in megaflops of reductions to condensed forms on an IBM POWER2 model 590
Following the reduction of a dense (or band) symmetric matrix to tridiagonal form T,
we must compute the eigenvalues and (optionally) eigenvectors of T.
Computing the eigenvalues of T alone (using LAPACK routine SSTERF ) requires
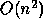 flops, whereas the reduction routine SSYTRD does
flops, whereas the reduction routine SSYTRD does 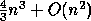 flops. So eventually the cost of finding eigenvalues
alone becomes small compared to the cost of reduction. However, SSTERF
does only scalar floating point operations, without scope for the BLAS,
so n may have to be large before SSYTRD is slower than SSTERF.
flops. So eventually the cost of finding eigenvalues
alone becomes small compared to the cost of reduction. However, SSTERF
does only scalar floating point operations, without scope for the BLAS,
so n may have to be large before SSYTRD is slower than SSTERF.
Version 2.0 of LAPACK includes a new algorithm, SSTEDC , for finding all eigenvalues and eigenvectors of n. The new algorithm can exploit Level 2 and 3 BLAS, whereas the previous algorithm, SSTEQR , could not. Furthermore, SSTEDC usually does many fewer flops than SSTEQR, so the speedup is compounded. Briefly, SSTEDC works as follows (for details, see [67][47]). The tridiagonal matrix T is written as
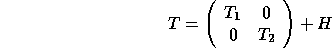
where 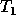 and
and 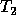 are tridiagonal, and H is a very simple rank-one matrix.
Then the eigenvalues and eigenvectors of
are tridiagonal, and H is a very simple rank-one matrix.
Then the eigenvalues and eigenvectors of 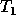 and
and 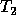 are found by applying
the algorithm recursively; this yields
are found by applying
the algorithm recursively; this yields 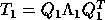 and
and
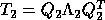 , where
, where 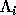 is a diagonal matrix of eigenvalues,
and the columns of
is a diagonal matrix of eigenvalues,
and the columns of  are orthonormal eigenvectors. Thus
are orthonormal eigenvectors. Thus

where 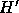 is again a simple rank-one matrix. The eigenvalues and eigenvectors
of
is again a simple rank-one matrix. The eigenvalues and eigenvectors
of 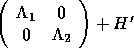 may be found
using
may be found
using 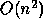 scalar operations, yielding
scalar operations, yielding
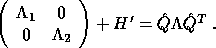 Substituting this into the last displayed expression yields
Substituting this into the last displayed expression yields
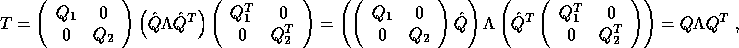
where the diagonals of 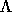 are the desired eigenvalues of T, and the columns
of
are the desired eigenvalues of T, and the columns
of 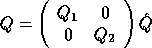 are the eigenvectors.
Almost all the work is done in the two matrix multiplies of
are the eigenvectors.
Almost all the work is done in the two matrix multiplies of 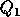 and
and 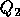 times
times
 , which is done using the Level 3 BLAS.
, which is done using the Level 3 BLAS.
The same recursive algorithm can be developed for the singular value decomposition of the bidiagonal matrix resulting from reducing a dense matrix with SGEBRD. This software will be completed for a future release of LAPACK. The current LAPACK algorithm for the bidiagonal singular values decomposition, SBDSQR , does not use the Level 2 or Level 3 BLAS.
For computing the eigenvalues and eigenvectors of a Hessenberg matrix-or rather for computing its Schur factorization- yet another flavour of block algorithm has been developed: a multishift QR iteration [8]. Whereas the traditional EISPACK routine HQR uses a double shift (and the corresponding complex routine COMQR uses a single shift), the multishift algorithm uses block shifts of higher order. It has been found that often the total number of operations decreases as the order of shift is increased until a minimum is reached typically between 4 and 8; for higher orders the number of operations increases quite rapidly. On many machines the speed of applying the shift increases steadily with the order, and the optimum order of shift is typically in the range 8-16. Note however that the performance can be very sensitive to the choice of the order of shift; it also depends on the numerical properties of the matrix. Dubrulle [37] has studied the practical performance of the algorithm, while Watkins and Elsner [77] discuss its theoretical asymptotic convergence rate.
Finally, we note that research into block algorithms for symmetric and nonsymmetric eigenproblems continues [55][9], and future versions of LAPACK will be updated to contain the best algorithms available.