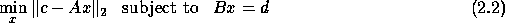
Driver routines are provided for two types of generalized linear least squares problems.
The first is
where A is an m-by-m matrix and B is a p-by-n matrix,
c is a given m-vector, and d is a given p-vector,
with p < = n < = m + p.
This is
called a linear equality-constrained least squares problem (LSE).
The routine xGGLSE
solves this problem using the generalized RQ
(GRQ) factorization, on the
assumptions that B has full row rank p and
the matrix 
has full column rank n.
Under these assumptions, the problem LSE has a unique solution.
The second generalized linear least squares problem is
where A is an n-by-m matrix, B is an n-by-p matrix, and d is a given n-vector, with m < = n < = m + p. This is sometimes called a general (Gauss-Markov) linear model problem (GLM). When B = I, the problem reduces to an ordinary linear least squares problem. When B is square and nonsingular, the GLM problem is equivalent to the weighted linear least squares problem:
The routine xGGGLM solves this problem using the generalized QR (GQR) factorization, on the assumptions that A has full column rank m, and the matrix (A , B) has full row rank n. Under these assumptions, the problem is always consistent, and there are unique solutions x and y. The driver routines for generalized linear least squares problems are listed in Table 2.4.
------------------------------------------------------------------
Single precision Double precision
Operation real complex real complex
------------------------------------------------------------------
solve LSE problem using GQR SGGLSE CGGLSE DGGLSE ZGGLSE
solve GLM problem using GQR SGGGLM CGGGLM DGGGLM ZGGGLM
------------------------------------------------------------------
Table 2.4: Driver routines for generalized linear least squares problems