The linear least squares problem is:
where A is an m-by-n matrix, b is a given m element vector and x is the n element solution vector.
In the most usual case m > = n and rank(A) = n, and in this case the solution to problem (2.1) is unique, and the problem is also referred to as finding a least squares solution to an overdetermined system of linear equations.
When m < n and rank(A) = m, there are an infinite number
of solutions x
which exactly satisfy b - Ax = 0. In this case it is often useful to find
the unique solution x which minimizes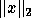 
,
and the problem
is referred to as finding a minimum norm solution to an
underdetermined system of linear equations.
The driver routine xGELS
solves problem (2.1) on the assumption that
rank(A) = min(m , n) -- in other words, A has full rank -
finding a least squares solution of an overdetermined system
when m > n, and a minimum norm solution of an underdetermined system
when m < n.
xGELS uses a QR or LQ factorization of A, and also allows A to be
replaced by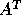 
in the statement of the problem (or by 
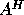if A is
complex).
In the general case when we may have
rank(A) < min(m , n) -- in other words,
A may be rank-deficient -
we seek the minimum norm least squares solution x
which minimizes both 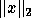and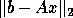 
.
The driver routines xGELSX and xGELSS solve this general formulation of problem 2.1, allowing for the possibility that A is rank-deficient; xGELSX uses a complete orthogonal factorization of A, while xGELSS uses the singular value decomposition of A.
The LLS driver routines are listed in Table 2.3.
All three routines allow several right hand side vectors b and corresponding
solutions x to be handled in a single call, storing these vectors as columns
of matrices B and X, respectively.
Note however that problem 2.1 is solved for
each right hand side vector independently; this is not the same as
finding a matrix X which minimizes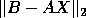 
.
-------------------------------------------------------------------
Single precision Double precision
Operation real complex real complex
-------------------------------------------------------------------
solve LLS using QR or SGELS CGELS DGELS ZGELS
LQ factorization
solve LLS using complete SGELSX CGELSX DGELSX ZGELSX
orthogonal factorization
solve LLS using SVD SGELSS CGELSS DGELSS ZGELSS
-------------------------------------------------------------------
Table 2.3: Driver routines for linear least squares problems