Basic Ideas
Y. Saad

Most of the standard eigenvalue algorithms exploit projection processes in order to extract approximate eigenvectors from a given subspace. The basic idea of a projection method is to extract an approximate eigenvector from a specified low-dimensional subspace. Certain conditions are required in order to be able to extract these approximations. Once these conditions are expressed, a small matrix eigenvalue problem is obtained.

A somewhat trivial but interesting illustration of the use of projection is when the dominant eigenvalue of a matrix is computed by the power method as follows:

select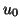 $u_{0}$
for $i=0, \ldots,$ until convergence do:
$u = A u_i$
$u_{i+1} = u / \Vert u\Vert _2$
$\wtd\lambda_{i+1} = u^T_{i+1} A u_{i+1}$

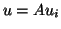
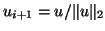
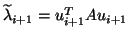
In the simplest case when the dominant eigenvalue, i.e., the eigenvalue with largest modulus, is real and simple, the pair $u_{i+1}, \wtd\lambda_{i+1}$ converges to the eigenvector and associated (largest in modulus) eigenvalue under mild assumptions on the initial vector. If this eigenvalue is complex and real arithmetic is used, then the algorithm will fail to converge. It is possible to work in complex arithmetic by introducing a complex initial vector, and in this way convergence will be recovered. However, it is also possible to extract these eigenvectors by working in real arithmetic. This is based on the observation that two successive iterates $u_{i}$ and $u_{i+1}$ will tend to belong to the subspace spanned by the two complex conjugate eigenvectors associated with the desired eigenvalue. Let $u_{i}$ and $u_{i+1}$ be denoted by $v_1$ and $v_2$, respectively. To extract the approximate eigenvectors, we write them as linear combinations of $v_1$ and $v_2$:

$$\tlu = \eta_1 v_1 + \eta_2 v_2.$$

We seek a vector and a scalar $\tla$ such that

$$A \tlu = \tla \tlu.$$

This is an underdetermined system. In addition to $\tla$, two degrees of freedom are available, namely, the scalars $\eta_1$ and $\eta_2$. They can be determined by imposing two constraints. It is most common to express these constraints in the form of orthogonality conditions. These are the Galerkin conditions, which require that the residual $r = A \tlu - \tla \tlu$ be orthogonal to the subspace of approximation, namely, to $v_1$ and $v_2$:

$$A \tlu - \tla \tlu \orth v_1 , \qquad A \tlu - \tla \tlu \orth v_2 .$$

Define the $n \times 2$ matrix $V \bydef [v_1,v_2]$ and call $y$ the 2-vector of unknowns $\eta_1, \eta_2$, i.e., $y = (\eta_1, \eta_2)^T$. Then, clearly $\tlu = V y$ and the above equations give rise to

$$( A - \tla I ) V y \perp v_1 , \qquad ( A - \tla I ) V y \perp v_2$$

or equivalently,

$$V^{\ast} ( A - \tla I ) V y = 0 .$$

This yields the $2 \times 2$ generalized eigenvalue problem:

$$V^{\ast} A V y = \tla \ V^{\ast} V y .$$

The (complex) approximate pair of conjugate eigenvalues obtained from this problem will now converge under the same conditions as those stated for the real case. The iteration uses real vectors, yet the process is able to extract complex eigenvalues. Clearly, the approximate eigenvectors are complex but they need not be computed in complex arithmetic. This is because the (real) basis $[v_1, v_2]$ is also a suitable basis for the complex plane spanned by $v_1$ and $v_2$.

The above idea can now be generalized from two dimensions to $m$ dimensions. Thus, a projection method consists of approximating the exact eigenvector $u$, by a vector $\tlu$ belonging to some subspace $\KK$ referred to as the subspace of approximants or the right subspace. If the subspace has dimension $m$, this gives $m$ degrees of freedom and the next step is to impose $m$ constraints to be able to extract a unique solution. This is done by imposing the so-called Petrov-Galerkin condition that the residual vector of $\tlu$ be orthogonal to some subspace $\LL$, referred to as the left subspace. Though this may seem artificial, we can distinguish between two broad classes of projection methods. In an orthogonal projection technique the subspace $\LL$ is the same as $\KK$. In an oblique projection method $\LL$ is different from $\KK$ and can be completely unrelated to it.

The construction of $\KK$ can be done in different ways. The above-suggested generalization of the power method leads, if one works with all generated vectors, to the Krylov subspace methods, that is, methods that seek the solution in the subspace

$${\cal K}^m(A,u_0) = {\rm span}\{ u_0, Au_0, \ldots , A^{m-1}u_0\},$$

the so-called Krylov subspace. One can also attempt to force these vectors to be more in the direction of the desired eigenvector, by inexact inversion techniques (preconditioning), which leads to Davidson-type methods. Alternatively, one can start with a set (block) of vectors instead of a single vector and this leads to the so-called block variants of these subspace methods.