The polynomial
![]() is the
characteristic polynomial of
is the
characteristic polynomial of ![]() .
The degree of
.
The degree of ![]() is at most
is at most ![]() .
The roots of
.
The roots of ![]() are called the finite eigenvalues of
are called the finite eigenvalues of ![]() .
If the degree of
.
If the degree of ![]() is
is ![]() , we say that
, we say that
![]() has
has ![]() infinite eigenvalues too.
For example,
infinite eigenvalues too.
For example,
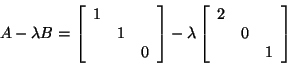
If ![]() is a finite eigenvalue,
a nonzero vector
is a finite eigenvalue,
a nonzero vector ![]() satisfying
satisfying
![]() is a (right) eigenvector
for the eigenvalue
is a (right) eigenvector
for the eigenvalue ![]() .
A nonzero vector
.
A nonzero vector ![]() satisfying
satisfying
![]() is a left eigenvector.
is a left eigenvector.
If ![]() is an eigenvalue, nonzero vectors
is an eigenvalue, nonzero vectors ![]() and
and ![]() satisfying
satisfying
![]() and
and ![]() are called right and left eigenvectors, respectively.
are called right and left eigenvectors, respectively.
An ![]() by
by ![]() pencil
pencil ![]() need not have
need not have ![]() independent eigenvectors.
The simplest example is
independent eigenvectors.
The simplest example is
![]() , which is defined
in equation (2.3) and discussed in §2.5.1.
The fact that
, which is defined
in equation (2.3) and discussed in §2.5.1.
The fact that ![]() independent eigenvectors may not exist
(though there is at least one for each distinct eigenvalue) will
necessarily complicate both theory and algorithms for the GNHEP.
independent eigenvectors may not exist
(though there is at least one for each distinct eigenvalue) will
necessarily complicate both theory and algorithms for the GNHEP.
Since the eigenvalues may be complex or infinite, there is no fixed way to order them.
Nonetheless, it is convenient to number them as
![]() ,
with corresponding right eigenvectors
,
with corresponding right eigenvectors
![]() and left eigenvectors
and left eigenvectors
![]() (if they exist).
(if they exist).