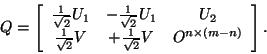
In other words,
This decomposition generalizes to the cases where ![]() is singular or
is singular or
![]() by
by ![]() ,
to a decomposition equivalent to the SVD of
,
to a decomposition equivalent to the SVD of ![]() (the product SVD),
and indeed to decompositions of arbitrary products of the form
(the product SVD),
and indeed to decompositions of arbitrary products of the form
![]() [108].
[108].
If
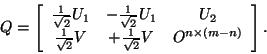
This decomposition generalizes to the cases where ![]() is singular or
is singular or
![]() by
by ![]() ,
to a decomposition equivalent to the SVD of
,
to a decomposition equivalent to the SVD of ![]() (the product SVD),
and indeed to decompositions of arbitrary products of the form
(the product SVD),
and indeed to decompositions of arbitrary products of the form
![]() [108].
[108].