 |
We attempt to simultaneously diagonalize two noisy (random
noise) versions
of diag(1:10) and diag(1:10)^2. Our initial
point is a small random perturbation of the identity.
>> !cp examples/simdiag/*.m .
>> randn('state',0);
>> [A,B] = noisy;
>> parameters(A,B);
>> Y0 = guess;
>> [fn,Yn] = sg_min(Y0,'frcg','euclidean');
iter grad F(Y) flops
0 2.887592e+03 9.671138e+02 30940
1 1.419011e+03 2.411349e+02 343392
2 6.199732e+02 7.601495e+01 718792
3 3.051636e+02 3.300591e+01 1106535
4 2.538995e+02 2.078422e+01 1518380
5 1.440247e+02 1.258174e+01 1923273
6 1.189063e+02 9.500450e+00 2332153
7 9.279907e+01 7.309071e+00 2743897
8 8.483878e+01 6.093323e+00 3161294
9 7.763100e+01 4.117233e+00 3609412
10 7.448803e+01 3.220241e+00 4026633
11 6.404668e+01 2.328540e+00 4439092
.......(many iterations later).......
169 2.196881e-06 4.010660e-07 67843218
170 2.309773e-06 4.010660e-07 68212219
171 2.435095e-06 4.010660e-07 68558476
172 1.763263e-06 4.010660e-07 68946596
173 2.081518e-06 4.010660e-07 69314166
174 1.251419e-06 4.010660e-07 69639992
175 1.474565e-06 4.010660e-07 70028565
176 8.949991e-07 4.010660e-07 70353929
177 8.506853e-07 4.010660e-07 70742988
178 7.154996e-07 4.010660e-07 71068090
179 8.003997e-07 4.010660e-07 71395085
180 3.164977e-07 4.010660e-07 71721113
181 3.701357e-07 4.010660e-07 72030590
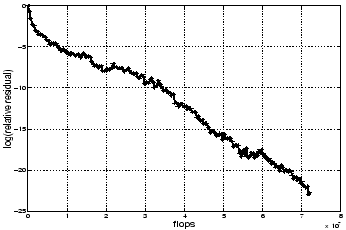
Figure 9.6 shows the convergence curve for this run.