




Next: Trace Minimization
Up: Sample Problems and Their
Previous: The Procrustes Problem
Contents
Index
Nearest-Jordan Structure
Now suppose that the  block in the Procrustes problem is allowed
to vary with
block in the Procrustes problem is allowed
to vary with 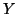 . Moreover, suppose that
. Moreover, suppose that 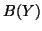 is in the nearest
staircase form to
is in the nearest
staircase form to 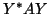 ; that is,
; that is,
for fixed block sizes,
where the *-elements are the corresponding matrix elements of 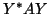 and
the
and
the 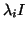 blocks are either fixed or determined by some heuristic, e.g.,
taking the average trace of the blocks they replace in
blocks are either fixed or determined by some heuristic, e.g.,
taking the average trace of the blocks they replace in 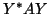 . Then
a minimization of
. Then
a minimization of
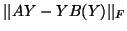 finds the nearest matrix as a particular
Jordan structure, where the structure is determined by the block sizes
and the eigenvalues are
finds the nearest matrix as a particular
Jordan structure, where the structure is determined by the block sizes
and the eigenvalues are 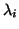 .
When the
.
When the 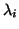 are fixed, we call this the orbit problem,
and when the
are fixed, we call this the orbit problem,
and when the 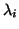 are selected by the heuristic given we call
this the bundle problem.
are selected by the heuristic given we call
this the bundle problem.
Such a problem can be useful in regularizing the computation of Jordan
structures of matrices with ill-conditioned eigenvalues.
The form of the differential of 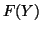 , surprisingly, is the same as that
of
, surprisingly, is the same as that
of 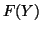 for the Procrustes problem
for the Procrustes problem
This is because
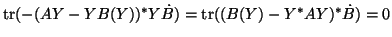 for the
for the  selected as above for either the orbit or the bundle case, where
selected as above for either the orbit or the bundle case, where
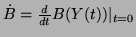 .
.
In contrast, the form of the second
derivatives is a bit more complicated, since  now depends on
now depends on 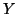 :
:
where
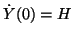 ,
,
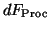 is just short for the Procrustes (
is just short for the Procrustes ( constant)
part of the second derivative, and
constant)
part of the second derivative, and
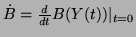 , which is
the staircase part of
, which is
the staircase part of 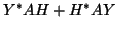 (with trace averages
or zeros on the diagonal depending on whether bundle or orbit).
(with trace averages
or zeros on the diagonal depending on whether bundle or orbit).





Next: Trace Minimization
Up: Sample Problems and Their
Previous: The Procrustes Problem
Contents
Index
Susan Blackford
2000-11-20
![]() block in the Procrustes problem is allowed
to vary with
block in the Procrustes problem is allowed
to vary with ![]() . Moreover, suppose that
. Moreover, suppose that ![]() is in the nearest
staircase form to
is in the nearest
staircase form to ![]() ; that is,
; that is,
![\begin{displaymath}B(Y) = \left[ \begin{array}{ccc}
\lambda_1 I & * & * \cr
0 & \lambda_2 I & * \cr
0 & 0 & \dots
\end{array}\right]\end{displaymath}](img3436.png)
![]() , surprisingly, is the same as that
of
, surprisingly, is the same as that
of ![]() for the Procrustes problem
for the Procrustes problem
![]() now depends on
now depends on ![]() :
: