




Next: Nearest-Jordan Structure
Up: Sample Problems and Their
Previous: Sample Problems and Their
Contents
Index
The Procrustes Problem
The Procrustes problem (see [158]) is the minimization of
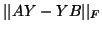 for constant
for constant  and
and  over the manifold
over the manifold 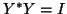 .
This minimization determines the nearest matrix
.
This minimization determines the nearest matrix 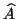 to
to  for
which
for
which
i.e. the columns of  span an invariant subspace of
span an invariant subspace of 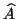 .
.
The differential of
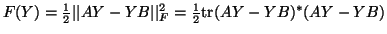 is given by
is given by
This can be derived following the process outlined above.
Observe that
The second derivative of 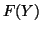 is given by the equation
is given by the equation
where
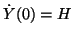 ,
which can be obtained by varying the expression for
,
which can be obtained by varying the expression for 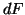 .
.
Susan Blackford
2000-11-20
![]() for constant
for constant ![]() and
and ![]() over the manifold
over the manifold ![]() .
This minimization determines the nearest matrix
.
This minimization determines the nearest matrix ![]() to
to ![]() for
which
for
which
![]() is given by
is given by
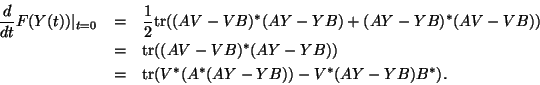
![]() is given by the equation
is given by the equation