GUPTRI Algorithm

The algorithm for computing the GUPTRI form is based on two reductions (staircase forms) [121]. The first is the $RZ$-staircase form that reveals the right singular structure and the Jordan structure of the zero eigenvalue of $A - \lambda B$.

The $RZ$-algorithm uses a finite number of unitary equivalence transformations, where in step $k~(= 1, 2, \ldots)$, $n_k =$ dimension of the column null space of $A^{(k)}$ and $n_k - r_k=$ dimension of the intersecting column null space of $A^{(k)}$ and $B^{(k)}$ are determined. Here, $A^{(1)} = A$ and $B^{(1)} = B$, and $\{A^{(k)}, B^{(k)}\}$ for $k > 1$ correspond to the deflated matrix pair obtained after the equivalence transformation in step $k-1$. The structure indices ($RZ$-indices) display the Kronecker structure as follows:

$$\begin{eqnarray*} n_k - r_k &=&{\rm ~ number~of~} L_{k-1} {\rm ~blocks}, \\ r_k - n_{k+1} &=&{\rm ~ number~of~} J_{k}(0) {\rm ~blocks}. \end{eqnarray*}$$

Before we state the general case we consider a $6\times 8$ matrix pencil in $RZ$-staircase form:

$$\begin{eqnarray*} A_{rz} - \lambda B_{rz} \!\! &\!\! = \!\! & \!\! \left[ \begi... ... y}& y & y \\ \hline 0 & 0 & 0 & 0 & 0 & 0 & 0 &{\bf z} \emat . \end{eqnarray*}$$

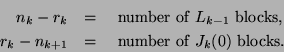
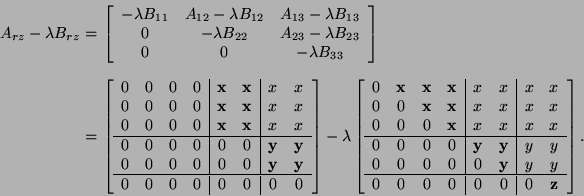
Nonzero entries after each deflation are marked with a unique letter (x from first step, y from second step, etc.), and they appear in bold or italic. The superdiagonal blocks of $A_{rz}$ have full column rank and the diagonal blocks of $B_{rz}$ have full row rank. The nonzero entries of the full rank blocks are marked in bold font. We use this notation in later examples as well.

The diagonal blocks (defining the ``stairs'') in $A_{rz} - \lambda B_{rz}$ are of size $r_i \times n_i$ and show the following information:

$$\begin{eqnarray*} &&\!\!\! n_1 = 4 = {\rm dim}~{\cal N}(A^{(1)}), \quad r_1 = 3 ... ...{(3)}), \\ [2mm] &&\!\!\! n_4 = 0 = {\rm dim}~{\cal N}(A^{(4)}). \end{eqnarray*}$$

Now, we can conclude that the KCF of $A_{rz} - \lambda B_{rz}$ is ${\rm diag}(L_0, L_2, J_1(0), J_3(0))$.

In general, let $A$ and $B$ be complex $m \times n$ matrices. Then it can be shown that there exist unitary matrices $U \: \in {\cal C}^{m \times m}$ and $V \: \in {\cal C}^{n \times n}$ such that the matrix pencil $A - \lambda B$ is transformed to the following so-called RZ-staircase form [121,122]: U^*(A - B)V = [

] - [

], where the staircase block structure of $A_{rz}$ and $B_{rz}$ reveals the right singular structure and the Jordan structure of the zero eigenvalue of $A - \lambda B$:

The subblocks in (8.37) and (8.38) have the following properties:

• $B_{ii}$ is $r_i \times n_i$ and $A_{i-1,i}, B_{i-1,i}$ are $r_{i-1} \times n_i$, where $n_i \geq r_i \geq n_{i+1} \geq r_{i+1}$.
• $B_{ii} = [ 0, R_{ii}]$, where $R_{ii}$ is $r_i \times r_i$ and upper triangular.
• $B_{ii}$ has full row rank $r_i$ for $i = 1, \ldots, j-1$.
• $A_{i-1,i}$ has full column rank $n_i$ for $i = 2, \ldots, j$.
• $A_{rest}$ and $B_{rest}$ are $r_{rest} \geq 0$ by $n_{rest} \geq 0$, where $A_{rest}$ has full column rank if it appears.

Three cases can appear in the $RZ$-staircase form depending on $r_{rest}$ and $n_{rest}$:

1. $r_{rest} > 0$ and $n_{rest} > 0$, in which case $A_{rest}$ has full column rank.
2. $r_{rest} > 0$ and $n_{rest} = 0$.
3. $r_{rest} = n_{rest} = 0$.
   

In cases 1 and 2, the blocks appear as in (8.37) and the remaining Kronecker structure of $A - \lambda B$ is in $A_{rest} - \lambda B_{rest}$. In case 3, $A_{rest} - \lambda B_{rest}$ does not exist in (8.37). In all three cases, it is possible that the $j$th block column of $A_{rz} - \lambda B_{rz}$ (8.38) does not appear; if it does, $A_{j-1,j}$ also has full column rank. For convenience, let $r_j = 0$.

We see that the $6\times 8$ example above corresponds to case 3 and that $A_{rz} - \lambda B_{rz}$ does not have a $j$th block column.

The second reduction is the $LI$ (left-infinity)-staircase form that reveals the left singular structure and the Jordan structure of the infinite eigenvalue of $A - \lambda B$. This dual staircase form is obtained by working from the southeast corner of $B - \mu A$ and replacing column compressions by row compressions in the $RZ$-algorithm. The block indices $n_i$ and $r_i$ are dimensions of corresponding row null spaces and define the $LI$-indices. Moreover, $n_k - r_k$ and $r_k - n_{k+1}$ are the number of $L_{k-1}^T$ and $N_{k}$ blocks, respectively.

Both the $RZ$-staircase and $LI$-staircase reductions give us two types of structure elements which must be separated to obtain the GUPTRI form. For example, the right singular structure and the Jordan structure of the zero eigenvalue are separated by first applying the $RZ$-staircase reduction to $B_{rz} - \mu A_{rz}$ and insisting on the same right minimal indices. Then we obtain $\{A_r, B_r\}$ and are left with a pencil, say, $A_2 - \lambda B_2$ corresponding to the zero eigenvalue. Finally, $\{A_z, B_z\}$ is obtained by transforming $A_2 - \lambda B_2$ to $RZ$-staircase form.

We return to the $6\times 8$ example and show the separated $R$-staircase and $Z$-staircase forms:

$$A_{r} - \lambda B_{r} = \bmat{cc\vert c\vert c} 0 & 0 & {\b... ... c} 0 &{\bf x}& x & x \\ \hline 0 & 0 &{\bf y}&{\bf z} \emat$$

and

$$A_{z} - \lambda B_{z} = \bmat{cc\vert c\vert c} 0 & 0 & {\b... ...ine 0 & 0 & {\bf y}& y \\ \hline 0 & 0 & 0 & {\bf z} \emat .$$

As for $A_{rz} - \lambda B_{rz}$, the superdiagonal blocks of $A_r$ and $A_z$ have full column rank and the diagonal blocks of $B_r$ and $B_z$ have full row rank. In the following table, the structure indices for the $RZ$-, $R$-, and $Z$-staircase forms of the $6\times 8$ example are summarized. We see that the $RZ$-staircase indices are the sum of the $R$- and $Z$-staircase indices, respectively.

$i$	1	2	3	4
$n_i$	4	2	2	0
$r_i$	3	2	1	0

$i$	1	2	3	4
$n_i$	2	1	1	0
$r_i$	1	1	0	0

$i$	1	2	3	4
$n_i$	2	1	1	0
$r_i$	2	1	1	0

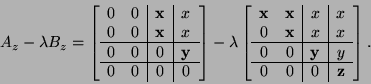
In summary, the GUPTRI algorithm for computing (8.34) and (8.35) comprises seven reduction steps. The first three steps apply the $RZ$-staircase reduction to different blocks of $A - \lambda B$, giving the right singular structure ( $A_r - \lambda B_r$) and the zero Jordan structure ( $A_z - \lambda B_z$) in the top left corner of $A$ and $B$. Similarly, the next three steps apply the $LI$-staircase reduction to different blocks of the remaining pencil, giving the infinite Jordan structure ( $A_i - \lambda B_i$) and the left singular structure ( $A_l - \lambda B_l$) in the bottom right corner of $A$ and $B$. Then a square regular pencil is left in the middle of the transformed pencil, which corresponds to the finite and nonzero eigenvalues of $A - \lambda B$. By applying the QZ algorithm to this pencil, the upper triangular block $A_f - \lambda B_f$ is obtained.