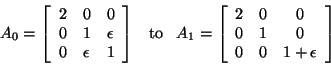Next: Specifying an Eigenproblem
Up: Hermitian Eigenproblems J.
Previous: Eigendecompositions
Contents
Index
Conditioning
The eigenvalues of  are always well-conditioned,
in the sense that changing
are always well-conditioned,
in the sense that changing  in norm by at most
in norm by at most 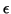 can change
any eigenvalue by at most
can change
any eigenvalue by at most 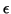 .
We refer to §4.8 for technical definitions.
.
We refer to §4.8 for technical definitions.
This is adequate for most purposes, unless the user is
interested in the leading digits of a small eigenvalue, one
less than or equal to 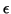 in magnitude. For example, computing
in magnitude. For example, computing
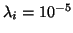 to within plus or minus
to within plus or minus
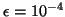 means
that no leading digits of the computed
means
that no leading digits of the computed 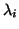 may be correct.
See [114,118] for a discussion of the sensitivity of small
eigenvalues and of when their leading digits may be computed accurately.
may be correct.
See [114,118] for a discussion of the sensitivity of small
eigenvalues and of when their leading digits may be computed accurately.
Eigenvectors and eigenspaces, on the other hand, can be ill-conditioned.
For example, changing
rotates the two eigenvectors corresponding to the two eigenvalues near 1
by 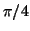 , no matter how small
, no matter how small 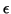 is. Thus they are very sensitive
to small changes.
The condition number of an eigenvector depends on the gap
between its eigenvalue and the closest other eigenvalue: the smaller the gap the
more sensitive the eigenvectors.
In this example the two eigenvalues near 1
are very close, so their gaps are small and their eigenvectors are sensitive.
But the two-dimensional invariant subspace they span is
very insensitive to changes in
is. Thus they are very sensitive
to small changes.
The condition number of an eigenvector depends on the gap
between its eigenvalue and the closest other eigenvalue: the smaller the gap the
more sensitive the eigenvectors.
In this example the two eigenvalues near 1
are very close, so their gaps are small and their eigenvectors are sensitive.
But the two-dimensional invariant subspace they span is
very insensitive to changes in  (because their eigenvalues, both near 1, are
very far from the next closest eigenvalue, at 2).
So when eigenvectors corresponding to a cluster of close eigenvalues
are too ill-conditioned, the user may want to compute a basis of the
invariant subspace they span instead of individual eigenvectors.
(because their eigenvalues, both near 1, are
very far from the next closest eigenvalue, at 2).
So when eigenvectors corresponding to a cluster of close eigenvalues
are too ill-conditioned, the user may want to compute a basis of the
invariant subspace they span instead of individual eigenvectors.





Next: Specifying an Eigenproblem
Up: Hermitian Eigenproblems J.
Previous: Eigendecompositions
Contents
Index
Susan Blackford
2000-11-20
![]() are always well-conditioned,
in the sense that changing
are always well-conditioned,
in the sense that changing ![]() in norm by at most
in norm by at most ![]() can change
any eigenvalue by at most
can change
any eigenvalue by at most ![]() .
We refer to §4.8 for technical definitions.
.
We refer to §4.8 for technical definitions.
![]() in magnitude. For example, computing
in magnitude. For example, computing
![]() to within plus or minus
to within plus or minus
![]() means
that no leading digits of the computed
means
that no leading digits of the computed ![]() may be correct.
See [114,118] for a discussion of the sensitivity of small
eigenvalues and of when their leading digits may be computed accurately.
may be correct.
See [114,118] for a discussion of the sensitivity of small
eigenvalues and of when their leading digits may be computed accurately.