




Next: Practical Algorithm
Up: Block Arnoldi Method
Previous: Block Arnoldi Method
Contents
Index
Let  be a matrix of order
be a matrix of order 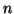 and
and 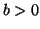 be the block size. We say that
be the block size. We say that
![\begin{displaymath}
A V_{[m]} = V_{[m]} H_{[m]} + F_m E^{\ast}_m
\end{displaymath}](img2109.png) |
(135) |
is a block Arnoldi reduction of length 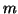 when
when
![$V_{[m]}^\ast AV_{[m]}=H_{[m]}$](img2110.png) is a band upper Hessenberg matrix
of order
is a band upper Hessenberg matrix
of order 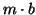 ,
,
![$V_{[m]}^\ast V_{[m]}= I_{m b}$](img2112.png) , and
, and
![$V_{[m]}^\ast F_m=0.$](img2113.png) For us, a band upper Hessenberg matrix is an upper triangular matrix
with
For us, a band upper Hessenberg matrix is an upper triangular matrix
with 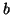 subdiagonals.
The columns of
subdiagonals.
The columns of
![$V_{[m]} = [V_1,V_2,\ldots,V_m]$](img2114.png) are an orthogonal basis for the block Krylov subspace
are an orthogonal basis for the block Krylov subspace
If
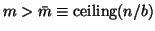 , then
, then 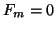 and
and
![$H_{[m]}$](img2118.png) is the
orthogonal reduction of
is the
orthogonal reduction of  into banded upper Hessenberg form.
We assume, for the moment, that
into banded upper Hessenberg form.
We assume, for the moment, that 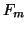 is of full rank and
further suppose that the elements on the diagonal of
is of full rank and
further suppose that the elements on the diagonal of 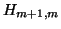 are
positive.
Thus, a straightforward extension of the implicit Q
theorem [198, pp. 367-368]
gives that
are
positive.
Thus, a straightforward extension of the implicit Q
theorem [198, pp. 367-368]
gives that 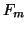 is (uniquely) specified by the starting block
is (uniquely) specified by the starting block 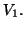 Note that if
Note that if 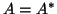 , then
, then ![$H_{[m]}$](img2118.png) is a block tridiagonal matrix.
Algorithm 7.11 lists an algorithm to compute a block Arnoldi
reduction.
is a block tridiagonal matrix.
Algorithm 7.11 lists an algorithm to compute a block Arnoldi
reduction.
![\begin{algorithm}{Extending a Block Arnoldi Reduction
}
{
\begin{tabbing}
(nr)s...
...m]}^\ast W \\
H_{m+1,m+1}
\end{array}\right] $\end{tabbing}}
\end{algorithm}](img2123.png)
We now comment on some steps of Algorithm 7.11.
- (1)
- Here the QR factorization is computed via an iterated
CGS algorithm using a possible correction step.
See [96] for details and the simple test used to determine
whether a correction step is necessary.
One benefit of this scheme is that it allows the use of the Level 2
BLAS [133] matrix-vector multiplication
subroutine xGEMV (also see §10.2).
Moreover, this scheme also gives a simple way to fill out a rank-deficient
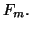 For instance,
if a third step of orthogonalization is needed when generating column
For instance,
if a third step of orthogonalization is needed when generating column 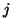 of
of
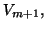 then the corresponding column of
then the corresponding column of 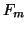 is linearly dependent
on the previous
is linearly dependent
on the previous 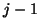 columns of
columns of 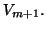 The
The 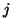 th diagonal element of
th diagonal element of 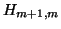 is set to zero, and a random unit vector is orthogonalized against
is set to zero, and a random unit vector is orthogonalized against ![$V_{[m]}$](img2127.png) and the first
and the first 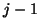 columns of
columns of 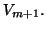
- (3)
- This step allows the application of
 to a group of vectors. This might
prove essential when accessing
to a group of vectors. This might
prove essential when accessing  is expensive. Clearly, the goal is
to amortize the cost of applying
is expensive. Clearly, the goal is
to amortize the cost of applying  over several vectors.
over several vectors.
- (4)
- This allows the use of the Level 3 BLAS [134]
matrix-matrix multiplication subroutine xGEMM
for computing
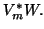
- (6)
- This is one step of block classical Gram-Schmidt (bCGR).
The Level 3 BLAS [134]
matrix-matrix multiplication subroutine xGEMM
is used for computing the rank-
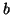 update needed
for the computation of
update needed
for the computation of 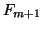 .
To ensure the orthogonality of
.
To ensure the orthogonality of 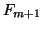 with
with 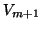 , a second step of
bCGR is performed except when
, a second step of
bCGR is performed except when 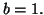 In this latter case, the simple test
in DGKS [96] is used to determine whether a second orthogonalization
step is needed. See [295] for details.
In this latter case, the simple test
in DGKS [96] is used to determine whether a second orthogonalization
step is needed. See [295] for details.
The scheme given for computing ![$V_{[m+1]}$](img2132.png) is equivalent to the one
proposed by Ruhe
is equivalent to the one
proposed by Ruhe
[375] (for symmetric matrices) and is the one
used by the implicitly restarted block Lanczos code [24].
Although the approach in [24] cleanly deals with the problem
of rank-deficient 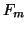 , the implementation does not exploit the
ability to apply
, the implementation does not exploit the
ability to apply  as in (3) above. Instead, as proposed
in [375],
as in (3) above. Instead, as proposed
in [375],  is applied to each column of
is applied to each column of 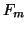 followed by
computing the corresponding column of
followed by
computing the corresponding column of 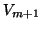 and
and ![$H_{[m+1]}.$](img2133.png) Our
implementation further reorganizes Ruhe's approach so that the
computation of the matrix of coefficients
Our
implementation further reorganizes Ruhe's approach so that the
computation of the matrix of coefficients
![$V_{[m]}^\ast W$](img2134.png) is
separated from the QR factorization of
is
separated from the QR factorization of 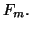 The advantage is that
steps (3)-(5) reduce the cost of I/O by a factor of the block size and
increase the amount of floating point operations per memory reference.
The advantage is that
steps (3)-(5) reduce the cost of I/O by a factor of the block size and
increase the amount of floating point operations per memory reference.





Next: Practical Algorithm
Up: Block Arnoldi Method
Previous: Block Arnoldi Method
Contents
Index
Susan Blackford
2000-11-20
![\begin{algorithm}{Extending a Block Arnoldi Reduction
}
{
\begin{tabbing}
(nr)s...
...m]}^\ast W \\
H_{m+1,m+1}
\end{array}\right] $\end{tabbing}}
\end{algorithm}](img2123.png)
![]() is equivalent to the one
proposed by Ruhe
is equivalent to the one
proposed by Ruhe
![]() , the implementation does not exploit the
ability to apply
, the implementation does not exploit the
ability to apply ![]() as in (3) above. Instead, as proposed
in [375],
as in (3) above. Instead, as proposed
in [375], ![]() is applied to each column of
is applied to each column of ![]() followed by
computing the corresponding column of
followed by
computing the corresponding column of ![]() and
and ![]() Our
implementation further reorganizes Ruhe's approach so that the
computation of the matrix of coefficients
Our
implementation further reorganizes Ruhe's approach so that the
computation of the matrix of coefficients
![]() is
separated from the QR factorization of
is
separated from the QR factorization of ![]() The advantage is that
steps (3)-(5) reduce the cost of I/O by a factor of the block size and
increase the amount of floating point operations per memory reference.
The advantage is that
steps (3)-(5) reduce the cost of I/O by a factor of the block size and
increase the amount of floating point operations per memory reference.