




Next: Eigenvector Computation with Spectral
Up: Orthogonal Deflating Transformation
Previous: Stability of .
Contents
Index
Although the basic deflation ideas of locking and purging are conceptually
straightforward, there are still a number of implementation details
and various strategies one might consider. In the end, some ad-hoc
decisions will have to be made. The deflation strategy adopted here is somewhat conservative
However, the performance appears to be quite reasonable in practice. In [420],
computational examples demonstrate that very low tolerances can be specified without missing multiple
or clustered eigenvalues.
The implementation details become quite involved and it is difficult to
convey the ideas by displaying code. Instead, we shall indicate the
main ideas of the strategy with a fairly high-level verbal description.
![\begin{algorithm}{Deflation for IRAM
}
{
\begin{enumerate}
\item [\rm (1)]
Lo...
... locked Ritz values, the
iteration is halted.
\end{enumerate}}
\end{algorithm}](img2077.png)
Implementation notes:
- (1)
- Initially, we work with an
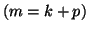 -step Arnoldi factorization and apply
-step Arnoldi factorization and apply
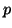 shifts per each implicit restart. Each time a Ritz value is locked,
it is advantageous to decrease the effective value
of
shifts per each implicit restart. Each time a Ritz value is locked,
it is advantageous to decrease the effective value
of 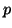 by 1
by 1
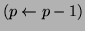 . This allows the polynomial filter to
have a larger relative magnitude on the Ritz value that is most likely
to converge next (see §7.6.3). Of course,
this must be limited to avoid lowering
the degree of the filter so much that it becomes ineffective. If
. This allows the polynomial filter to
have a larger relative magnitude on the Ritz value that is most likely
to converge next (see §7.6.3). Of course,
this must be limited to avoid lowering
the degree of the filter so much that it becomes ineffective. If 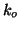 is
the number of locked Ritz values then the IRAM iteration takes place in
columns
is
the number of locked Ritz values then the IRAM iteration takes place in
columns 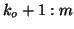 of
of 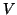 working within an
working within an 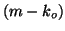 -length Arnoldi
factorization. The effective value of
-length Arnoldi
factorization. The effective value of 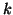 becomes
becomes 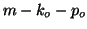 and
the effective value of
and
the effective value of 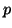 becomes
becomes 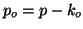 . This has two important
effects. The rate of convergence
as described in §7.6.3 is increased and the amount of work
per implicit restart is decreased.
. This has two important
effects. The rate of convergence
as described in §7.6.3 is increased and the amount of work
per implicit restart is decreased.
- (2)
- One might also wish to purge all converged but unwanted Ritz pairs at
this stage.
- (3)
- The purpose of introducing the random start vector here is to greatly increase
the likelihood of components in directions of wanted eigenvectors that have not
yet been found.
- (4)
- This ad-hoc stopping strategy is reasonable.
However, there is no ultimate assurance that the
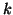 wanted eigenvalues have
all been found (especially in the case of clustered or multiple eigenvalues).
wanted eigenvalues have
all been found (especially in the case of clustered or multiple eigenvalues).





Next: Eigenvector Computation with Spectral
Up: Orthogonal Deflating Transformation
Previous: Stability of .
Contents
Index
Susan Blackford
2000-11-20
![\begin{algorithm}{Deflation for IRAM
}
{
\begin{enumerate}
\item [\rm (1)]
Lo...
... locked Ritz values, the
iteration is halted.
\end{enumerate}}
\end{algorithm}](img2077.png)