Convergence Properties

As convergence takes place, the subdiagonals of $H_k$ tend to zero and the most desired eigenvalue approximations appear as eigenvalues of the leading $k \times k$ block of $R$ in a Schur decomposition of $A$. The basis vectors $V_k$ tend to orthogonal Schur vectors.

An alternate interpretation stems from the fact that each of these shift cycles results in the implicit application of a polynomial in $A$ of degree $p$ to the starting vector. v_1 (A) v_1 with () = _j=1^p (- _j ). The roots of this polynomial are the shifts used in the QR process and these may be selected to enhance components of the starting vector in the direction of eigenvectors corresponding to desired eigenvalues and damp the components in unwanted directions. Of course, this is desirable because it forces the starting vector into an invariant subspace associated with the desired eigenvalues. This in turn forces $f_k$ to become small and hence convergence results. Full details may be found in [419].

There is a fairly straightforward intuitive explanation of how this repeated updating of the starting vector $v_1$ through implicit restarting might lead to convergence. If $v_1$ is expressed as a linear combination of eigenvectors $\{q_j\}$ of $A$, then

$$v_1 = \sum_{j=1}^n q_j \gamma_j \quad \Rightarrow \quad \psi(A)v_1 = \sum_{j=1}^n q_j \psi(\lambda_j) \gamma_j .$$

Applying the same polynomial (i.e., using the same shifts) repeatedly for $\ell$ iterations will result in the $j$th original expansion coefficient being attenuated by a factor

$$\left( \frac{\psi(\lambda_j)}{\psi(\lambda_1)} \right)^{\ell} \ ,$$

where the eigenvalues have been ordered according to decreasing values of $\vert\psi(\lambda_j)\vert$. The leading $k$ eigenvalues become dominant in this expansion and the remaining eigenvalues become less and less significant as the iteration proceeds. Hence, the starting vector $v_1$ is forced into an invariant subspace as desired. The adaptive choice provided with the exact shift mechanism further enhances the isolation of the wanted components in this expansion. Hence, the wanted eigenvalues are approximated better and better as the iteration proceeds.

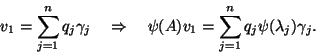
It is worth noting that if $m = n$ then $f_{m} = 0$ and this iteration is precisely the same as the implicitly shifted QR iteration. Even for $m<n$, the first $k$ columns of $V_m$ and the Hessenberg submatrix $H_m(1:k,1:k)$ are mathematically equivalent to the matrices that would appear in the full implicitly shifted QR iteration using the same shifts $\mu_j.$ In this sense, the implicitly restarted Arnoldi method may be viewed as a truncation of the implicitly shifted QR iteration. The fundamental difference is that the standard implicitly shifted QR iteration selects shifts to drive subdiagonal elements of $H_n$ to zero from the bottom up while the shift selection in the implicitly restarted Arnoldi method is made to drive subdiagonal elements of $H_m$ to zero from the top down. Shifted power-method-like convergence will be obtained.

When the exact shift strategy is used, implicit restarting can be viewed both as a means to damp unwanted components from the starting vector and also as directly forcing the starting vector to be a linear combination of wanted eigenvectors. See [419] for information on the convergence of IRAM and [22,421] for other possible shift strategies for Hermitian $A.$ The reader is referred to [292,333] for studies comparing implicit restarting with other schemes.