




Next: Software Availability
Up: Single- and Multiple-Vector Iterations
Previous: Inverse Iteration
Contents
Index
Subspace Iteration
The subspace iteration methods, also called simultaneous iteration methods,
for HEPs
can also be generalized for the NHEP.
Algorithm 7.2 is a modification of the subspace iteration
method of §4.3.4 for the HEP.
It includes deflation (locking) for computing
the 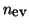 dominant eigenvalues. Since eigenvalues for
NHEPs can be very ill-conditioned, we
impose a more stringent convergence criterion.
dominant eigenvalues. Since eigenvalues for
NHEPs can be very ill-conditioned, we
impose a more stringent convergence criterion.
We now describe some implementation details.
- (1)
- The initial starting matrix
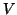 should be constructed
to be dominant in eigenvector directions of interest to
accelerate convergence. In case no such information is known
a priori, a random matrix is as good a choice as any other.
should be constructed
to be dominant in eigenvector directions of interest to
accelerate convergence. In case no such information is known
a priori, a random matrix is as good a choice as any other.
- (3)
- The iteration parameter
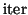 is introduced to reduce the costly orthonormalization
computation as much as possible. However,
is introduced to reduce the costly orthonormalization
computation as much as possible. However, 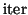 must not be too large lest one lose numerical accuracy in
the computation of the matrix
must not be too large lest one lose numerical accuracy in
the computation of the matrix 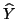 , leading to
inaccurate computation of some of the eigenvalues.
A typical value of
, leading to
inaccurate computation of some of the eigenvalues.
A typical value of 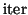 is 3 to 5.
is 3 to 5.
- (6)-(13)
- The convergence criterion in the above algorithm
checks for convergence only for groups of eigenvalues that
have nearly the same modulus. The diagonal blocks in step
(6) are ordered from top to bottom, with block
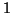 at the
top of
at the
top of 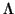 . In step (12), convergence
testing is stopped as soon as the first block of eigenvalues
in
. In step (12), convergence
testing is stopped as soon as the first block of eigenvalues
in 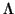 fails to converge.
fails to converge.
- (16)
- The iteration parameter
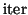 should be chosen to
minimize orthonormalization cost while maintaining a
reasonable amount of numerical accuracy.
should be chosen to
minimize orthonormalization cost while maintaining a
reasonable amount of numerical accuracy.
If eigenvalues near a shift 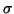 are desired, and a
factorization of
are desired, and a
factorization of
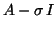 can be easily obtained,
then one can apply the above algorithm to
can be easily obtained,
then one can apply the above algorithm to
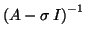 . The eigenvalues near
. The eigenvalues near 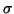 will
converge faster.
will
converge faster.
One can also use polynomial acceleration to speed up the
computation by replacing the power 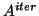 by a
polynomial
by a
polynomial
![$T_{iter} [ (A - \sigma I) / \rho ] $](img1890.png) in which
in which 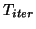 is the Chebyshev polynomial of the first kind of degree
is the Chebyshev polynomial of the first kind of degree
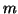 , and
, and 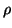 is an estimate of the spectral radius of
is an estimate of the spectral radius of
 .
.
Much of the material in this section is based on Bai and
Stewart [37] and Saad [387]. For further
discussion on subspace iteration, the reader is referred to
Wilkinson [457] and Stewart [422].





Next: Software Availability
Up: Single- and Multiple-Vector Iterations
Previous: Inverse Iteration
Contents
Index
Susan Blackford
2000-11-20
![]() dominant eigenvalues. Since eigenvalues for
NHEPs can be very ill-conditioned, we
impose a more stringent convergence criterion.
dominant eigenvalues. Since eigenvalues for
NHEPs can be very ill-conditioned, we
impose a more stringent convergence criterion.
![]() are desired, and a
factorization of
are desired, and a
factorization of
![]() can be easily obtained,
then one can apply the above algorithm to
can be easily obtained,
then one can apply the above algorithm to
![]() . The eigenvalues near
. The eigenvalues near ![]() will
converge faster.
will
converge faster.
![]() by a
polynomial
by a
polynomial
![]() in which
in which ![]() is the Chebyshev polynomial of the first kind of degree
is the Chebyshev polynomial of the first kind of degree
![]() , and
, and ![]() is an estimate of the spectral radius of
is an estimate of the spectral radius of
![]() .
.