Accuracy of Eigenvalues Computed after Balancing

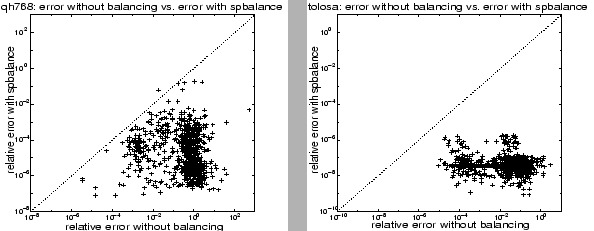
We conclude with a few examples showing the accuracy to which eigenvalues are computed, by dense and sparse eigensolvers, with and without balancing. This is the ``bottom line,'' showing how much balancing helps the overall eigenvalue computation process.

To study the accuracy of computed eigenvalues we need to know the true eigenvalues. For these experiments we computed the ``true'' eigenvalues in double precision, first using SPBALANCE to locate and balance the individual diagonal blocks of the matrix, then using a dense eigensolver to find the eigenvalues of each diagonal block separately. We then compared eigenvalues computed in single precision to these ``true'' eigenvalues.

Figures 7.1 and 7.2 plot the relative error in the eigenvalues calculated with balancing against the error in the eigenvalues calculated without balancing. Crosses below the dotted diagonal line represent eigenvalues calculated more accurately with balancing; the further a cross lies below the dotted line, the greater the difference in eigenvalue accuracy with and without balancing.

Figure 7.1: Relative accuracy of eigenvalues computed with and without direct balancing for the QH$768$ and TOLOSA matrices.

Figure 7.1 clearly shows that SPBALANCE is effective in improving the accuracy to which most eigenvalues of the QH768 and TOLOSA matrices, described in [28], are computed, often by many orders of magnitude.

Figure 7.2: Relative accuracy of eigenvalues computed with and without Krylov balancing for the QH$768$ and TOLOSA matrices.

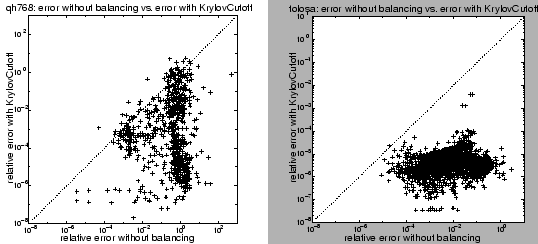Figure 7.2 shows that KRYLOVCUTOFF also improves the accuracy to which most eigenvalues of the QH768 and TOLOSA matrices are calculated, however the improvement is less than with the direct algorithm SPBALANCE.

In Figure 7.2, after Krylov-based balancing, the eigenvalues are computed using a dense eigensolver rather than a sparse solver; this is in order to isolate the effect of balancing. In practice, if a sparse matrix were given explicitly and one were willing to run an $O(n^3)$ dense eigensolver, one would precondition the matrix using SPBALANCE and not a Krylov-based method. In a more practical situation one would use KRYLOVCUTOFF to balance matrices whose eigenvalues are computed using algorithms using only matrix-vector multiplications.

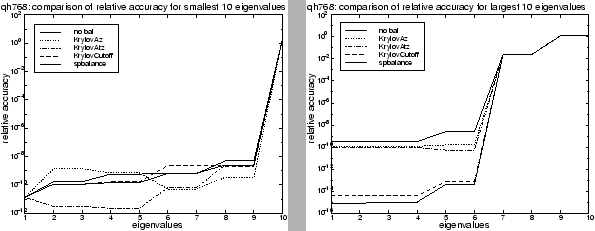
Figures 7.3 and 7.4 illustrate this more practical situation. They show the relative accuracy of the $10$ largest and smallest eigenvalues when calculated without balancing, with SPBALANCE, with KRYLOVCUTOFF, and with two other Krylov balancing algorithms described in [82] (KRYLOVAZ, which uses only $Az$, and KRYLOVATZ, which uses $Az$ and $A^Tz$ but no cutoff). The eigenvalues were computed in MATLAB using the eigs function, which uses the IRAM of §7.6.

Figure 7.3: Comparison of the relative accuracy of the largest and smallest (in magnitude) eigenvalues of the QH$768$ matrix, with different Krylov-based balancing algorithms, using the default settings of five iterations and a cutoff value of $10^{-8}$.

Figure 7.4: Comparison of the relative accuracy of the largest and smallest (in magnitude) eigenvalues of the TOLOSA matrix, with different Krylov-based balancing algorithms, using the default settings of five iterations and a cutoff value of $10^{-8}$.

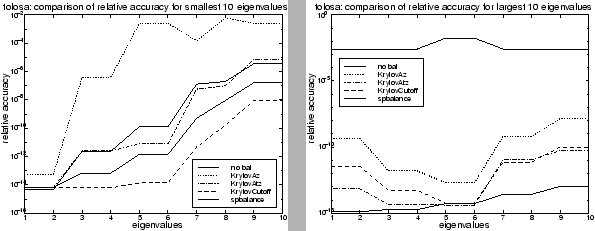Figure 7.3 shows little variation in the relative errors for the smallest eigenvalues of the QH768 matrix. However, for the largest eigenvalues KRYLOVCUTOFF does almost as well as SPBALANCE and significantly better than the results without balancing. On the TOLOSA matrix the smallest eigenvalues are computed most accurately after balancing by KRYLOVCUTOFF, even when compared to direct balancing. On the largest eigenvalues SPBALANCE is most effective, though all three Krylov balancing algorithms do significantly better than no balancing at all.