




Next: Variants
Up: Band Lanczos Method
Previous: Basic Properties
Contents
Index
Algorithm
A complete statement of the band Lanczos
algorithm for Hermitian matrices  is as follows.
is as follows.

Next, we discuss some of the steps of Algorithm 4.12
in more detail.
- (4)
- Generally, the decision on whether
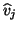 needs to be deflated should
be based on checking whether
needs to be deflated should
be based on checking whether
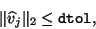 |
(51) |
where 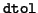 is a suitably chosen deflation tolerance.
The vector
is a suitably chosen deflation tolerance.
The vector 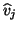 is then deflated if (4.42) is
satisfied.
In this case, the value
is then deflated if (4.42) is
satisfied.
In this case, the value 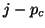 , if positive, is added to the index
set
, if positive, is added to the index
set 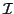 , which contains the indices of the nonzero rows
in the part
, which contains the indices of the nonzero rows
in the part
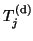 of
of 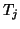 , and the current block size
is updated to
, and the current block size
is updated to 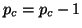 .
If
.
If 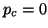 , the block Krylov sequence (4.27) is
exhausted, and the algorithm terminates naturally.
If
, the block Krylov sequence (4.27) is
exhausted, and the algorithm terminates naturally.
If 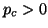 , the vector
, the vector 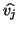 is deleted, the index
is deleted, the index 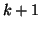 of each of the remaining candidate vectors
of each of the remaining candidate vectors 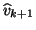 is
reset to
is
reset to 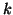 ,
and finally, the algorithm returns to step (3).
If (4.42) is not satisfied, no deflation is
necessary and the algorithm proceeds with step (5).
,
and finally, the algorithm returns to step (3).
If (4.42) is not satisfied, no deflation is
necessary and the algorithm proceeds with step (5).
Usually, in (4.42), one will choose a small tolerance
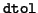 , such as
the square root of machine precision.
However,
, such as
the square root of machine precision.
However, 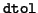 does not have to be small;
Algorithm 4.12 and its properties remain correct
for any choice of
does not have to be small;
Algorithm 4.12 and its properties remain correct
for any choice of 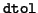 .
Note that the algorithm performs only exact deflation if one
sets
.
Note that the algorithm performs only exact deflation if one
sets 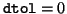 in (4.42).
in (4.42).
- (5)
- The vector
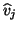 has passed the deflation check and is
now normalized to become the next Lanczos vector
has passed the deflation check and is
now normalized to become the next Lanczos vector 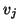 .
The normalization is such that
.
The normalization is such that
- (6)
- The remaining candidate vectors,
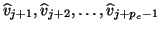 , are
explicitly orthogonalized against the latest Lanczos vector
, are
explicitly orthogonalized against the latest Lanczos vector 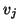 .
Note that in the first
.
Note that in the first 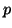 steps some
steps some 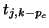 will have nonpositive
column index. They serve to make the starting basis orthonormal, but
need not be stored in the
will have nonpositive
column index. They serve to make the starting basis orthonormal, but
need not be stored in the 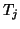 matrix.
matrix.
- (7)
- The block Krylov sequence is advanced by
computing a new candidate vector,
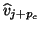 , as the
, as the
 -multiple of the latest Lanczos vector
-multiple of the latest Lanczos vector 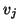 .
.
- (8)
- The vector
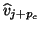 is
orthogonalized against the previous Lanczos vectors
is
orthogonalized against the previous Lanczos vectors
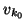 ,
, 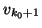 ,
, 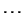 ,
, 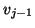 , where
, where
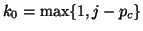 .
Here, we exploit the fact that the matrix
.
Here, we exploit the fact that the matrix
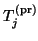 is Hermitian, and instead of explicitly computing
is Hermitian, and instead of explicitly computing 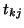 , we set
, we set
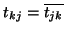 .
Note that the
.
Note that the 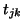 's were computed explicitly in step (6).
's were computed explicitly in step (6).
- (9)
- The vector
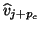 is explicitly
orthogonalized against the Lanczos vectors
is explicitly
orthogonalized against the Lanczos vectors 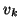 ,
,
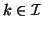 , and against
, and against 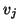 .
Note that modified Gram-Schmidt is used to do this orthogonalization.
.
Note that modified Gram-Schmidt is used to do this orthogonalization.
- (11)
- All the nonzero elements in the
 th row and
the
th row and
the  th column have now been computed, and they are added to the
matrix
th column have now been computed, and they are added to the
matrix
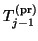 of the previous iteration
of the previous iteration 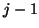 , to yield
the current matrix
, to yield
the current matrix
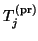 .
Here, we use the convention that entries
.
Here, we use the convention that entries 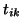 and
and 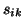 that are not explicitly defined in Algorithm 4.12 are set
to zero.
that are not explicitly defined in Algorithm 4.12 are set
to zero.
- (12)
- To test for convergence, the eigenvalues
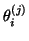 ,
,
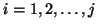 , of the Hermitian
, of the Hermitian 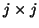 matrix
matrix
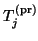 are computed, and the
algorithm is stopped if some of the
are computed, and the
algorithm is stopped if some of the
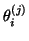 's are
good enough approximations to the desired eigenvalues of
's are
good enough approximations to the desired eigenvalues of  .
.





Next: Variants
Up: Band Lanczos Method
Previous: Basic Properties
Contents
Index
Susan Blackford
2000-11-20
![]() is as follows.
is as follows.
![]() , such as
the square root of machine precision.
However,
, such as
the square root of machine precision.
However, ![]() does not have to be small;
Algorithm 4.12 and its properties remain correct
for any choice of
does not have to be small;
Algorithm 4.12 and its properties remain correct
for any choice of ![]() .
Note that the algorithm performs only exact deflation if one
sets
.
Note that the algorithm performs only exact deflation if one
sets ![]() in (4.42).
in (4.42).